just answer this question, slide 44 is provided for reference

slide 44

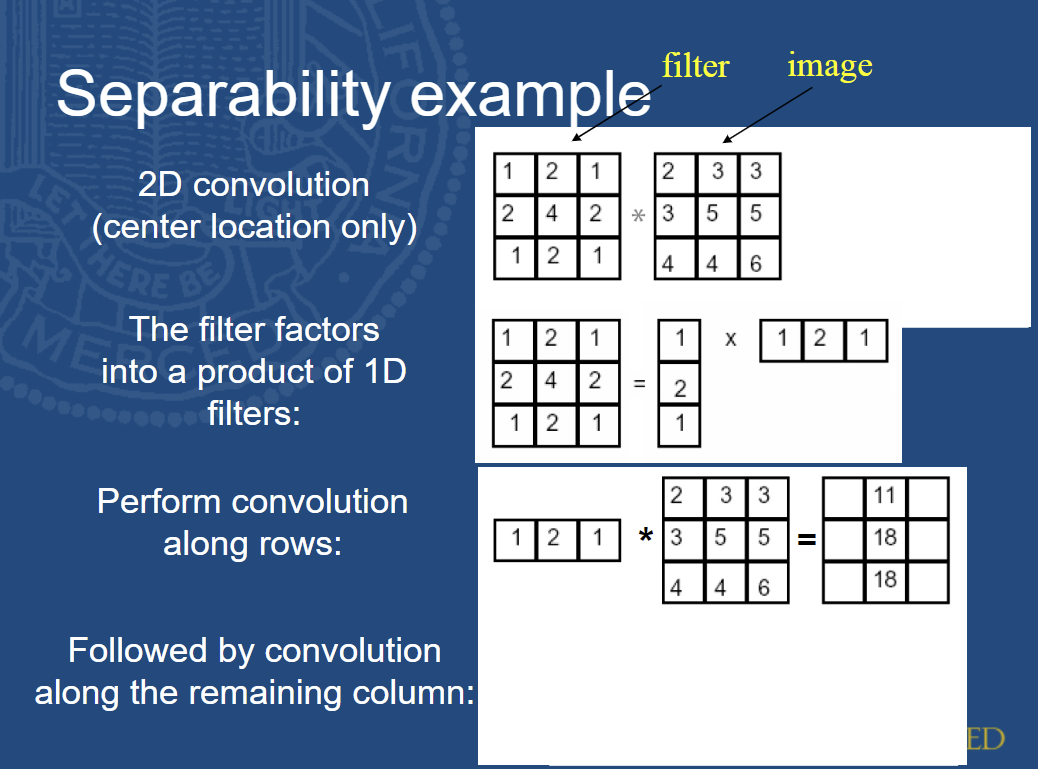
In the lecture today (slide 44), given the filter mask on the left (the matrix with 1, 2, 1, 2, 4, 2, 1,2,1) and the image region on the right (the matix with 2,3,3,3,5,5,4,4,6 ) Q1: If we use 2D filter, count the number of addition and multiplication that we need to filter this image. \begin{tabular}{|l|l|l|} \hline 2 & 3 & 3 \\ \hline 3 & 5 & 5 \\ \hline 4 & 4 & 6 \\ \hline \end{tabular} =6+20+10=4+8+6=2+6+3==36=6518 Since this filter is a separable one, it can be decomposed into two filters (one column filter and one row filter) \begin{tabular}{|l|l|l|} \hline 1 & 2 & 1 \\ \hline 2 & 4 & 2 \\ \hline 1 & 2 & 1 \\ \hline \end{tabular}=\begin{tabular}{|l|} \hline 1 \\ \hline 2 \\ \hline 1 \\ \hline \end{tabular} Separability ex 2D convolution (center location only) The filter factors into a product of 1D filters: Perform convolution along rows: Followed by convolution along the remaining column