just d

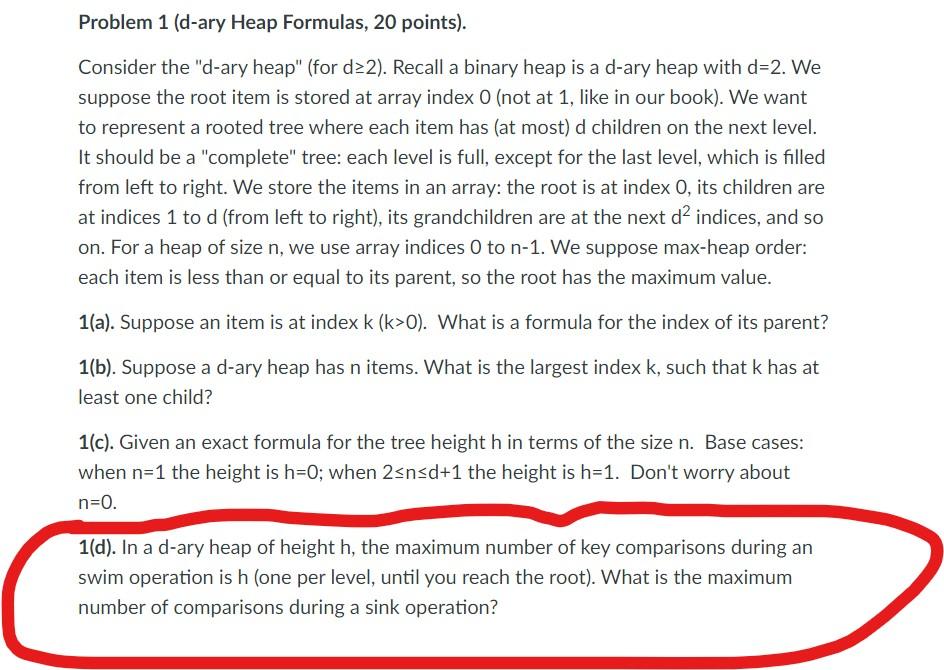
Problem 1 (d-ary Heap Formulas, 20 points). Consider the "d-ary heap" (for d2 ). Recall a binary heap is a d-ary heap with d=2. We suppose the root item is stored at array index 0 (not at 1 , like in our book). We want to represent a rooted tree where each item has (at most) d children on the next level. It should be a "complete" tree: each level is full, except for the last level, which is filled from left to right. We store the items in an array: the root is at index 0 , its children are at indices 1 to d (from left to right), its grandchildren are at the next d2 indices, and so on. For a heap of size n, we use array indices 0 to n1. We suppose max-heap order: each item is less than or equal to its parent, so the root has the maximum value. 1(a). Suppose an item is at index k(k>0). What is a formula for the index of its parent? 1(b). Suppose a d-ary heap has n items. What is the largest index k, such that k has at least one child? 1(c). Given an exact formula for the tree height h in terms of the size n. Base cases: when n=1 the height is h=0; when 2nd+1 the height is h=1. Don't worry about n=0. 1(d). In a d-ary heap of height h, the maximum number of key comparisons during an swim operation is h (one per level, until you reach the root). What is the maximum number of comparisons during a sink operation