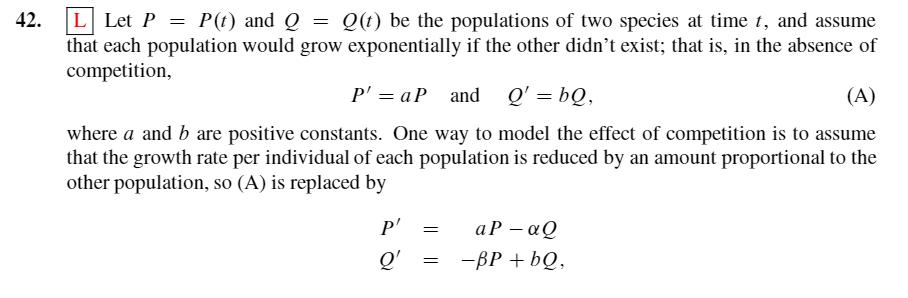
L Let P = P(1) and Q = Q(t) be the populations of two species at time t, and assume that each population would grow exponentially if the other didn't exist; that is, in the absence of competition, 42. P' = aP and Q' = bQ, (A) where a and b are positive constants. One way to model the effect of competition is to assume that the growth rate per individual of each population is reduced by an amount proportional to the other population, so (A) is replaced by P' aP - aQ Q' = -BP + bQ, where a and B are positive constants. (Since negative population doesn't make sense, this system holds only while P and Q are both positive.) Now suppose P(0) = Po > 0 and Q(0) = Qo > 0. (a) For several choices of a, b, a, and B, verify experimentally (by graphing trajectories of (A) in the P-Q plane) that there's a constant p >> 0 (depending upon a, b, a, and B) with the following properties: (i) If Qo > pPo, then P decreases monotonically to zero in finite time, during which Q remains positive. (ii) If Qo < pPo, then Q decreases monotonically to zero in finite time, during which P remains positive. (b) Conclude from (a) that exactly one of the species becomes extinct in finite time if Qo # pPo. Determine experimentally what happens if Qo = pPo. (c) Confirm your experimental results and determine y by expressing the eigenvalues and asso- ciated eigenvectors of -[ #] a A b in terms of a, b, a, and B, and applying the geometric arguments developed at the end of this section.