l need help, problem 17 question ( c, e, g, i)

MG305

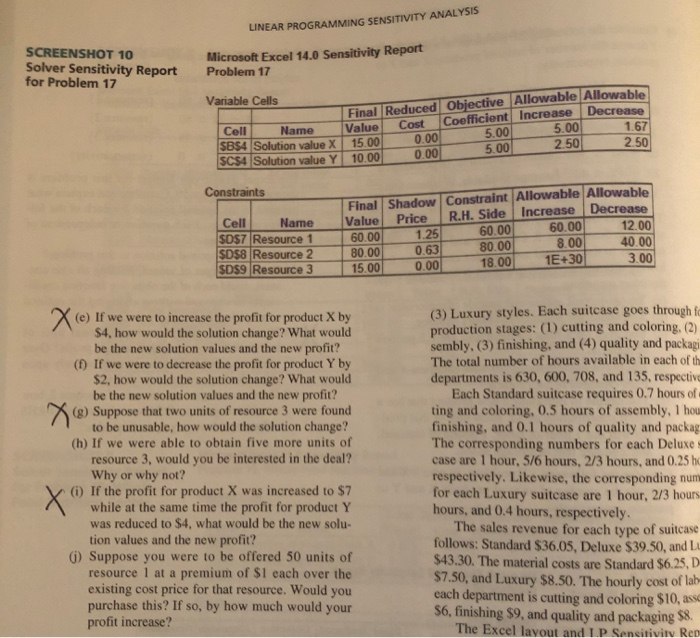
LINEAR PROGRAMMING SENSITIVITY ANALYSIS Consider the following LP problem, in which X and y denote the number of units of products X and Y to Maximize profit = $5X + $5Y produce, respectively: subject to the constraints Maximize profit = $4X + $5Y 2x + 3Y S 60 (resource 1) subject to the constraints 4X + 2Y = 80 (resource 2) X + 2Y = 10 (labor available, in hours) X 18 (resource 3) 6X + 6Y S 36 X,Y 2 0 (nonnegativity) (material available, in pounds) 8X + 4Y S 40 (storage available, in square feet) The Excel Sensitivity Report for this problem is X,Y 2 shown in Screenshot 10. Calculate and explain what 0 (nonnegativity) happens to the optimal solution for each of the fol The Excel Sensitivity Report for this problem is lowing situations. Each question is independent of shown in Screenshot 9. Calculate and explain what the other questions. happens to the optimal solution for each of the fol- (a) What is the optimal solution to this problem? lowing situations. Each question is independent of (b) For what ranges of values, holding all else con- the other questions. stant, could each of the objective function coeffi- (a) You acquire 2 additional pounds of material. cients be changed without changing the optimal solution? (b) You acquire 1.5 additional hours of labor. c) If we could obtain one additional unit of (c) You give up 1 hour of labor and get 1.5 pounds resource 1, how would it impact profit? Over of material. what range of RHS values could we rely upon (d) The profit contributions for both products X and this value? Y are changed to $4.75 each. (d) If we were to give up one unit of resource 2, how (e) You decide to introduce a new product that has a would it impact profit? Over what range of RHS profit contribution of $2. Each unit of this prod. values could we rely upon this value? uct will use 1 hour of labor, 1 pound of material, and 2 square feet of storage space. 17 Consider the following LP problem, in which X and Y denote the number of units of products X and Y to LINEAR PROGRAMMING SENSITIVITY ANALYSIS Microsoft Excel 14.0 Sensitivity Report SCREENSHOT 10 Solver Sensitivity Report for Problem 17 Problem 17 Variable Cells 5.00 Cell Name SBS4 Solution value X SCS4 Solution value Y Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 15.00 0 .00 5.00 10.00 0.00 5.00 2.50 2.50 Constraints Cell Name SD$7 Resource 1 $D$8 Resource 2 SD$9 Resource 3 Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 1.25 60.00 60.00 60.00 12.00 80.00 0.63 8.00 80.00 40.00 15.00 0.00 18.00 1E+30 3.00 X (e) If we were to increase the profit for product X by $4, how would the solution change? What would be the new solution values and the new profit? (1) If we were to decrease the profit for product Y by $2, how would the solution change? What would be the new solution values and the new profit? (8) Suppose that two units of resource 3 were found to be unusable, how would the solution change? (h) If we were able to obtain five more units of resource 3, would you be interested in the deal? Why or why not? V (i) If the profit for product X was increased to $7 while at the same time the profit for product Y was reduced to $4, what would be the new solu- tion values and the new profit? () Suppose you were to be offered 50 units of resource 1 at a premium of $1 each over the existing cost price for that resource. Would you purchase this? If so, by how much would your profit increase? (3) Luxury styles. Each suitcase goes through fo production stages: (1) cutting and coloring. (2) sembly. (3) finishing, and (4) quality and packagi The total number of hours available in each of th departments is 630, 600, 708, and 135, respective Each Standard suitcase requires 0.7 hours of ting and coloring, 0.5 hours of assembly, 1 hou finishing, and 0.1 hours of quality and packag The corresponding numbers for each Deluxe case are 1 hour, 5/6 hours, 2/3 hours, and 0.25 h respectively. Likewise, the corresponding num for each Luxury suitcase are 1 hour, 2/3 hours hours, and 0.4 hours, respectively. The sales revenue for each type of suitcase follows: Standard $36.05, Deluxe $39.50, and L $43.30. The material costs are Standard $6.25, D $7.50, and Luxury $8.50. The hourly cost of lab cach department is cutting and coloring $10, asse $6, finishing $9, and quality and packaging $8. The Excel layout and LP Sensitivity Red