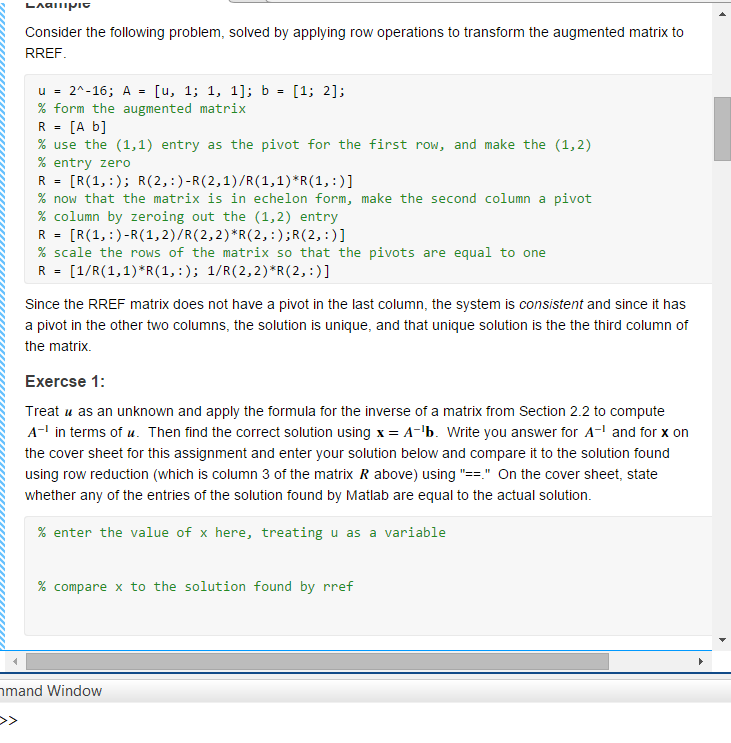
Laampic Consider the following problem, solved by applying row operations to transform the augmented matrix to RREF. u = 2^-16; A = [u, 1; 1, 1]; b = [1; 2]; % form the augmented matrix R = [A b] % use the (1,1) entry as the pivot for the first row, and make the (1,2) % entry zero R = [R(1,:); R(2,:)-R(2,1)/R(1,1)*R(1,:)] % now that the matrix is in echelon form, make the second column a pivot % column by zeroing out the (1,2) entry R = [R(1,:)-R(1,2)/R(2, 2)*R(2,:);R(2,:)] % scale the rows of the matrix so that the pivots are equal to one R = (1/R(1,1)*R(1,:); 1/R(2, 2)*R(2,:)] Since the RREF matrix does not have a pivot in the last column, the system is consistent and since it has a pivot in the other two columns, the solution is unique, and that unique solution is the the third column of the matrix. Exercse 1: Treat u as an unknown and apply the formula for the inverse of a matrix from Section 2.2 to compute A- in terms of u. Then find the correct solution using x= A-'b. Write you answer for A- and for x on the cover sheet for this assignment and enter your solution below and compare it to the solution found using row reduction (which is column 3 of the matrix R above) using "==." On the cover sheet, state whether any of the entries of the solution found by Matlab are equal to the actual solution. % enter the value of x here, treating u as a variable IETEI % compare x to the solution found by rref nmand Window Laampic Consider the following problem, solved by applying row operations to transform the augmented matrix to RREF. u = 2^-16; A = [u, 1; 1, 1]; b = [1; 2]; % form the augmented matrix R = [A b] % use the (1,1) entry as the pivot for the first row, and make the (1,2) % entry zero R = [R(1,:); R(2,:)-R(2,1)/R(1,1)*R(1,:)] % now that the matrix is in echelon form, make the second column a pivot % column by zeroing out the (1,2) entry R = [R(1,:)-R(1,2)/R(2, 2)*R(2,:);R(2,:)] % scale the rows of the matrix so that the pivots are equal to one R = (1/R(1,1)*R(1,:); 1/R(2, 2)*R(2,:)] Since the RREF matrix does not have a pivot in the last column, the system is consistent and since it has a pivot in the other two columns, the solution is unique, and that unique solution is the the third column of the matrix. Exercse 1: Treat u as an unknown and apply the formula for the inverse of a matrix from Section 2.2 to compute A- in terms of u. Then find the correct solution using x= A-'b. Write you answer for A- and for x on the cover sheet for this assignment and enter your solution below and compare it to the solution found using row reduction (which is column 3 of the matrix R above) using "==." On the cover sheet, state whether any of the entries of the solution found by Matlab are equal to the actual solution. % enter the value of x here, treating u as a variable IETEI % compare x to the solution found by rref nmand Window