LaTex question, analytic solution is given below

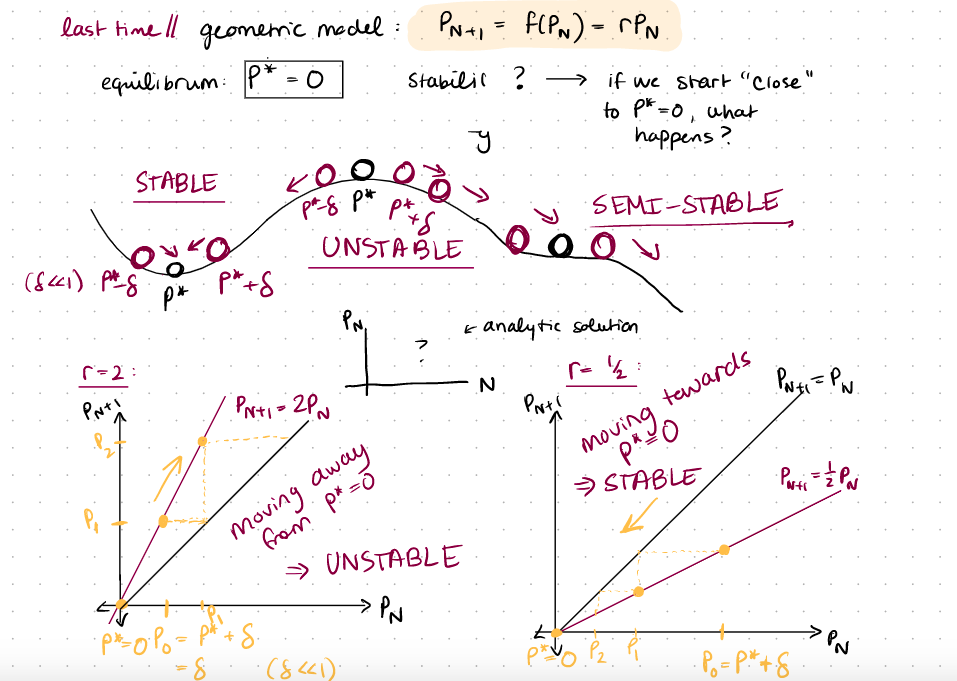
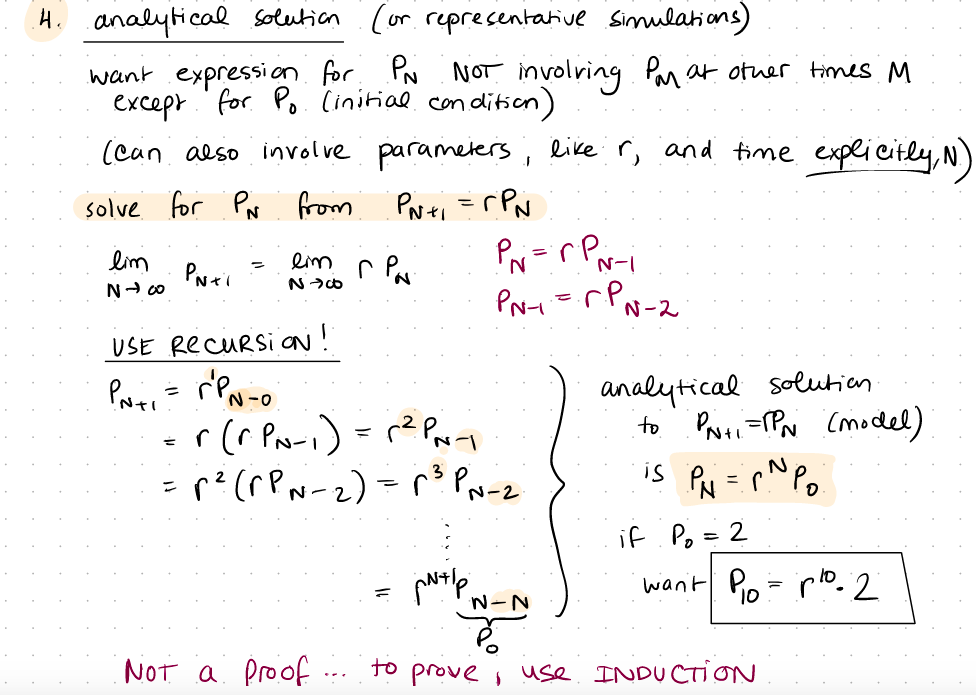
Problem 1: (2 pts) Using LaTex, typeset the analytic solution to the geometric growth model (model introduced in lecture 4, analytic solution discussed in lecture 5). Be sure to execute the cell so that the LaTeX typesetting actually displays nicely, instead of showing the LaTeX syntax. 2 Kos last time Il geometric model: PNti = (PN) = rPN equilibrum P* - Stabilir ? if we start "Close" to P*=o, what y happens? STABLE SEMI-STABLE UNSTABLE (8441) PAS P*+S p* Pri tanalytic solution N PNE=PN PNoti= 2PN pag. p* pa PAS +8 = 2: rah: Proti tewards Pnti moving to STABLE Parti - PN moving away from p*= >> UNSTABLE PN .p*o po = pk + S 8 :(821) t PN P P2P .Po =P*4.8 lim r Par - N00 N 06 H. analytical solution (or representative Simulations) want expression for PN NOT involving Por at other times mi except for Po. Cinitial condition) (can also involve parameters, like ry and time explicitly, N.) solve for PN from Prti = rPN lim PNrPoi PNti PN-=.r.PN-2 USE Recursia! analytical solution =r(& PN-1) = rPoi to Pri=PN (model) = P (PPN-2) = 13 PN-2 is PN = PNPO if Po=2 want Pio plo. 2 -2 Proti rPNO N 2 Antip N-N Not a proof ... to prove use INDUCTION