Learning Goal:

To determine the center of gravity of a composite body using the principle of superposition.

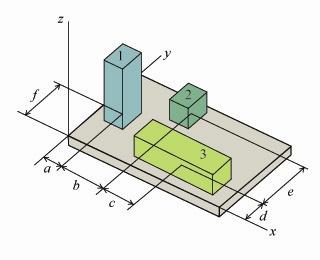
The layout shown is a representation of a machine shop. Components 1 and 2 have masses of m1=250kg and m2=215kg, respectively. Component 3 must be treated as a distributed load, which is w=175 kg/m2,determined by the area of contact between the component and the shop floor. The dimensions shown have been measured to be a=0.600 m, b=3.00 m,c=1.90 m, d=0.700 m, e=4.00 m, and f=1.10 m. These dimensions represent the x and ycomponents of the locations of the centers of gravity for the respective components. Component 3 has x,ycross-sectional dimensions of x3=1.10 m and y3=0.150 m. Assume the components experience uniform weight distribution in all principle directions. The dimensions a through f locate the centroid of the respective component from the y?z plane and x?zplane.

Determine the x component of the center of gravity of all the components.

Determine the y component of the center of gravity of all the components.

If the heights of the components are given as z1=1.90 m, z2=0.700 m, and z3=0.200 m, determine the z component of the center of gravity of all the components

Transcribed Image Text:

N X. N X.

Answer rating: 100% (QA)

To determine the center of gravity of a composite body you use the principle of moments which states that the moment of the weight of the entire body ... View the full answer