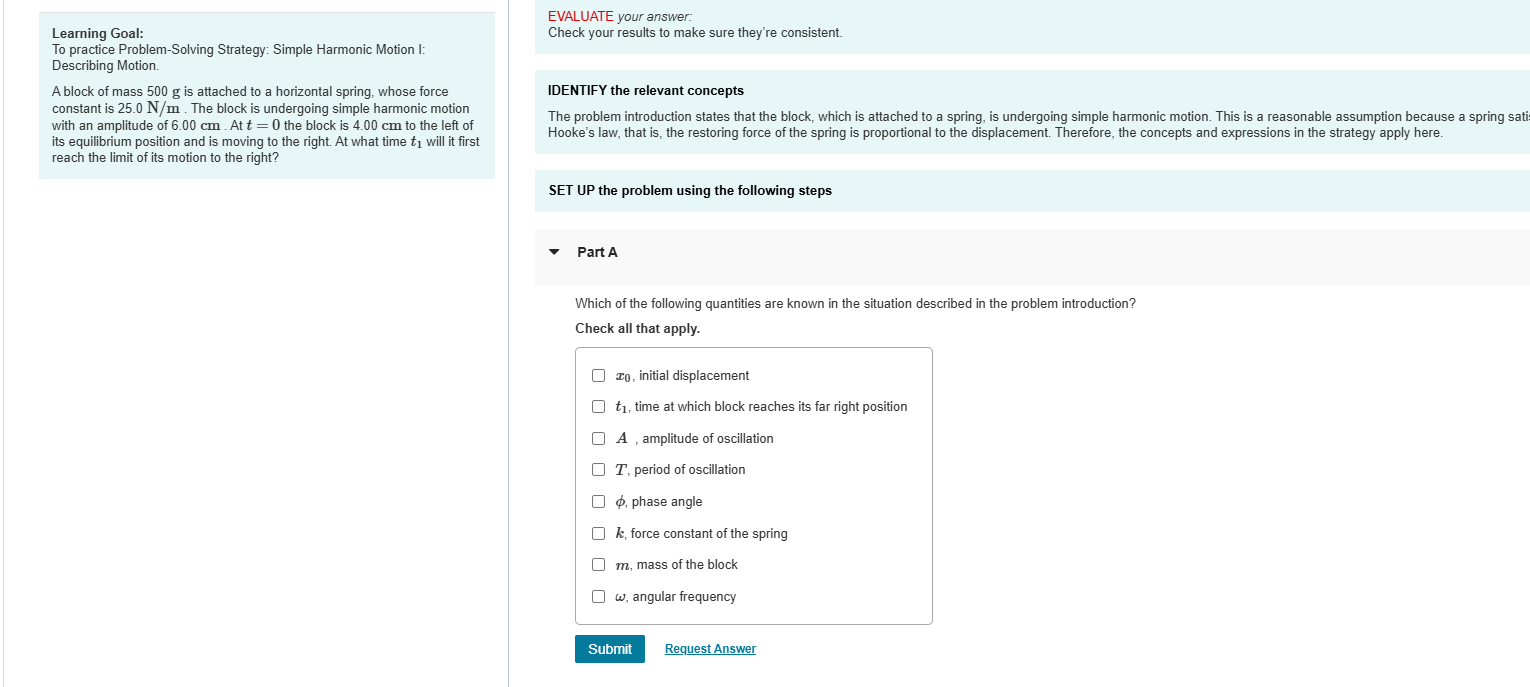
Learning Goal:

To practice Problem$-$Solving Strategy: Simple Harmonic Motion I: Describing Motion.

A block of mass $500$ g is attached to a horizontal spring, whose force constant is $\backslash (25\mathrm{.}0\backslash$mathrm$\{$~N$\}/\backslash$mathrm$\{$m$\}\backslash ).$ The block is undergoing simple harmonic motion with an amplitude of $6\mathrm{.}00$ cm $.$ At $\backslash ($ t$=0\backslash )$ the block is $4\mathrm{.}00$ cm to the left of its equilibrium position and is moving to the right. At what time $\backslash ($ t$\_\{1\}\backslash )$ will it first reach the limit of its motion to the right?

EVALUATE your answer:

Check your results to make sure they're consistent.

IDENTIFY the relevant concepts

The problem introduction states that the block, which is attached to a spring, is undergoing simple harmonic motion. This is a reasonable assumption because a spring sati Hooke's law, that is$,$ the restoring force of the spring is proportional to the displacement. Therefore, the concepts and expressions in the strategy apply here.

SET UP the problem using the following steps

Part A

Which of the following quantities are known in the situation described in the problem introduction?

Check all that apply.

$\backslash ($ x$\_\{0\}\backslash ),$ initial displacement

$\backslash ($ t$\_\{1\}\backslash ),$ time at which block reaches its far right position

A $,$ amplitude of oscillation

$\backslash ($ T $\backslash ),$ period of oscillation

$\backslash (\backslash$phi $\backslash ),$ phase angle

$\backslash (\backslash$boldsymbol$\{$k$\}\backslash ),$ force constant of the spring

$\backslash ($ m $\backslash ),$ mass of the block

$\backslash (\backslash$omega $\backslash ),$ angular frequency