Question: Learning Goal: To understand the notation, sign conventions, and use of the general slope - deflection equation. A section of a continuous beam ( Figure
Learning Goal:
To understand the notation, sign conventions, and use of the general slopedeflection equation.
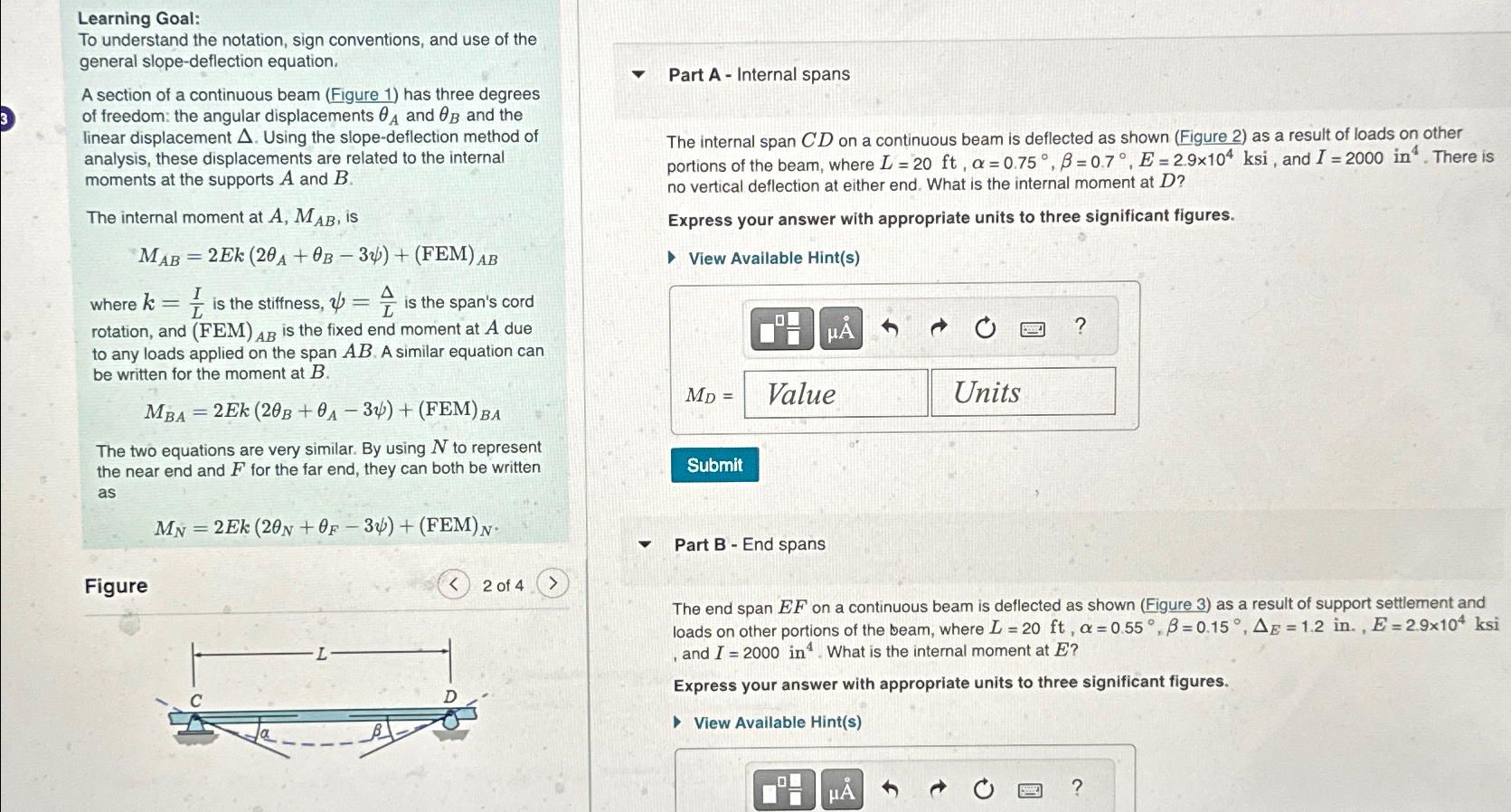
A section of a continuous beam Figure has three degrees of freedom: the angular displacements and and the linear displacement Using the slopedeflection method of analysis, these displacements are related to the internal moments at the supports A and
The internal moment at is
where is the stiffness, is the span's cord rotation, and FEM is the fixed end moment at A due to any loads applied on the span A similar equation can be written for the moment at
The two equations are very similar. By using to represent the near end and for the far end, they can both be written as
PLEASE SOLVE PART A USING GENERAL SLOPE DEFLECTION EQUATION
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


