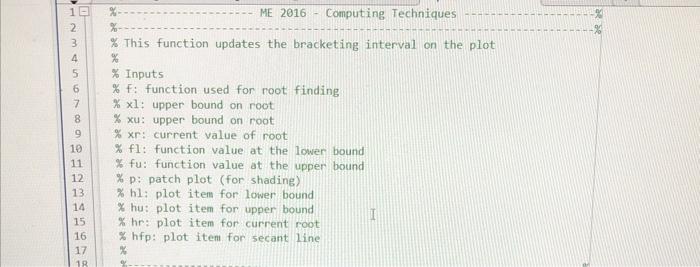
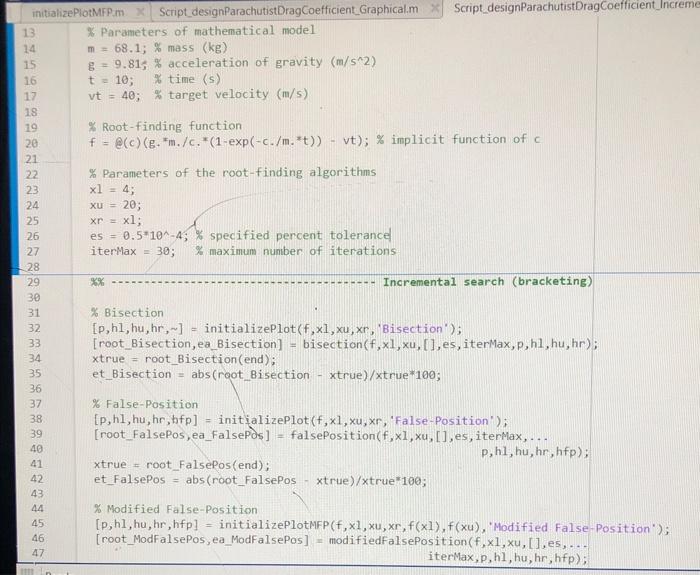
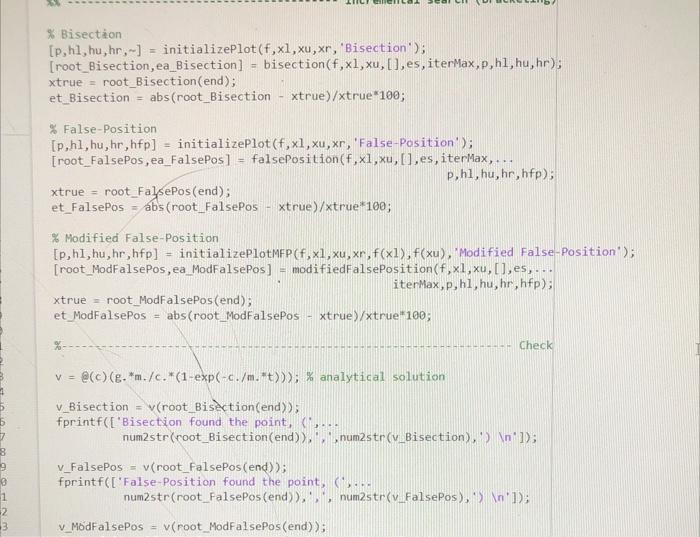
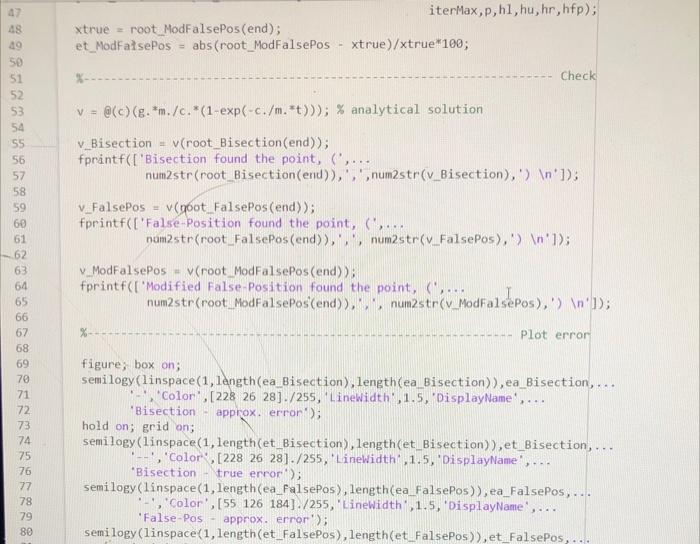
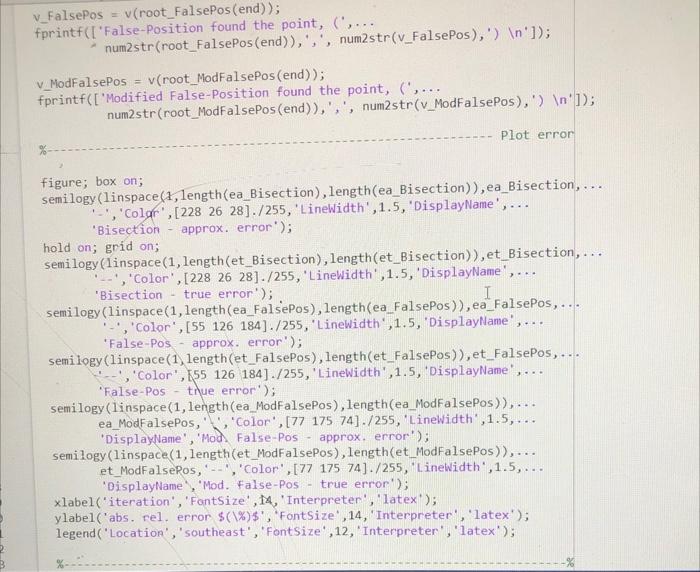
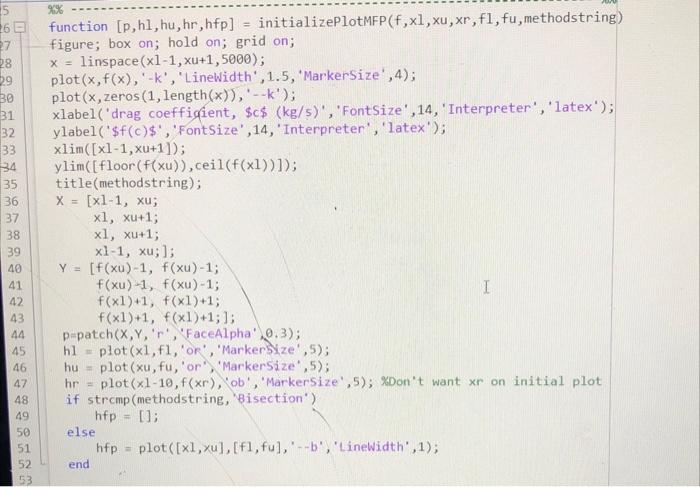
Learning Objectives - To implement Bisection and False-Position (bracketing) methods of root-finding and compare their convergence rates for a problem of interest. Problem description Figure 1: Schematic of circular cone frastum tunk holding water. The volume of water, V, in the cirenlar cone frustum tank in Figure 1 can be computed as V(h,r)3h(R12+r2+R1r) where the largest water radius, r, ean be expressed as a function of the water height, h, as r(h)R1+h(HR2R1) In (1) and (2), R1 and R2 are the bottom and top tank radii, respectively; and H is the height of the tank. Write a Matlab code that: (a) Uses the Bisection and Falso-Position methods to determine the depth of water, hh, so that the tank holds a target volume, VVt, of water. Hint: You will nead to define a function, f(h), that you urish to make zero. (b) Plots the solution, (h,V(h) ), found using each bracketing method (on one plot) on top of a curve of volume as a function of h, to verify that the correct root was found in both cascs. Hint: Your solutions should be two points that intersect the curve at the value of Vt. To draw the curve, you unll need to define a function, V(h), that differs from (1) in that it is a function of only h and not r. (c) Plots the absolute approximate peroent relative crror, |cal, over the iterations for each bracketing method (on a single plot with errot axis in log senle), to compare their relative convergence rates. Hint: Use somilogy. Your implementation Your code should be written in a seript file, Script_DepthOfWater.m, that defines a finction handle to the equation, f(h), of which we wish to find the root. The seript should call two separate function files, bisection.m and falsePosition.m, that accept a function handle to f(h) and implement the two bracketing methods in a general way (i.e, they should not be specific to the tank problem). These functions should print to the command window for each iteration (in an casily legible way - hint: use fprintf): the lower and upper bounds of the bracketing interval, the root estimate, the value of f(h), and the absolute approximate pereent relative error, a. Consider the following parameters when employing your root-finding methods. Use initial lower and upper bounds of the bracketing interval, he 0 and huH. In both cases, stop your algorithm when your absolute approximate perecnt relative error drops below a specified percent tolerance of 104 or when you reach a maximum of 30 iterations, whichever oecurs first. Consider tank parameters, H5m,R11m,R23m, and solve the problem for a target volume, Vt40m3 Your discussion In your report, comment on the relative convergence rates of the Bisection and False-Position methods. Which one converges faster? How do you know? Is this always expected to be the case (c.g., for other problems)? Learning Objectives - To implement Bisoction and False-Pesition (bracketing) methods of root-finding and compare their convergence rates for a problem of interest. Problem description Figure 1: Schenatic of citcular cone frust um tank holding water. The volume of water, V, in the circular cone frustum tank in Fugure 1 can be computed as V(h,r)=3h(R12+r2+R1r). where the largest water radits, r, can be expressed as a function of the water height, h, as r(h)=R1+h(IIR2R1). In (1) and (2), R1 and R2 are the bottom and top tank radii, respertively; and is the height of the tank. Write a Matlab code that: (a) Uses the Bisection and False-Position methods to determine the depth of water, h=h, so that the tank holds a turget volume, V=Vt, of water. Ilint: You sell nond to define a function, f(h), that you wish to make sero. (b) Plots the solution, (h,V(h) ), found using each hrackrting method (on one plot) on top of a curve of volume as a function of h, to verify thut the correct root was found in both cases. Ifint: Your solutions should be two points that intersoct the curve at the calue of Vt. To dras the curve, you will nond to define a function, V(h), that differs from (1) in that it is a function of only h and not r. (c) Plots the ahsolute approximate percent relative error, F. over the iterations for each bracketing method (on a single plot with error axis in log scale), to compare their relative convergence rates. Ilint: Use aemilogy. Your implementation Your code should be written in a seript file, Script.DepthOfWater.m, that defines a function handlasto the equation, f(h), of which we wish to find the root. The script should call two separate function files, bisection.m and falsePosition.m, that acept a function handle to f(h) and implement the two bracketing methods in a general way (i.e., they should not be specifie to the tank problem). These functions should print to the command window for each iteration (in an easily legible way - hint: use f printf): the lower and upper bounds of the bracketing interval, the root estimste, the value of f(h), and the ahsolute approximate percent relative error, Fa. Consider the following parameters when employing your root-finding methods. Use initial lower and upper bounds of the hracketing interval, h0 and hk=II. In both cases, stop your algorithm when your absolute approximate pereent relative error drops below a spocified perocnt tolerance of E2=104 or when you reach a maximum of 30 iterations, whichever pecurs fint. Consider tank parameters, H=5m,R11m,R2=3m, and solve the problem for a target volume, Vt=40m3. Your discussion In your report, comment on the relative convergener rates of the Bisection and False-Position methods. Which one converges faster? How do you know? Is the always expected to be the case (c.g., for other problems)? Deliverables Please place all files described below (c.g. .docx, .pdf, m ) in i xipped folder and upload to Canvas using the following naming convention: "IIW \#-FamilyName_FintName zip." (a) Professionally-formatted report. Plas provide a bricf description of the problem, the function you are finding the root of (f(h)), images of the two plots outpat by your code, a screcnshot of the conmand window output from your code, and your discussion. Be sure to format your report professionally. Each of your plots should include meaningful axis labels with units (when appropriate), a legible legend, and marker/line styles to make the curves/points casily distinguishable. Matlab:s "grid on" and "box on" commands are also suggested. Your report should include a header/footer with your name, date, course number, assignment number, and page numbers. (b) Professionally-formatted source code. Include Script_DepthOrWater.m, bisection.m, falsePosition.m, and any other functions (if any) that you wrote to complete the assignment. Please be sure that your code runs directly upon download of your zip file. Be sure to format your code professionally. At the top of each seript/function, include your name, the date, and a description of the file - for functions also define all input and output variables. Use comments and indenting for code readability. ME 2016 - Computing Techniques % This function updates the bracketing interval on the plot \% Paraneters of mathematical model v_FalsePos =v( root_FalsePos(end )); fprintf(I'False-Position found the point, ( ', num2str(root_FalsePos(end)), ;, num2str(v_FalsePos), ) ]); v ModFalsePos =v( root ModFalsePos(end)); fprintf(['Modified False-Position found the point, (,, num2str(root_ModFalsePos (end)),',', num2str(v_ModFalsePos), ') ]); Plot error figure; box on; semilogy (linspace(1, length(ea_Bisection), length(ea_Bisection)), ea_Bisection, ... '. ', 'Colgr', [2282628]./255, 'Linewidth', 1.5, 'DisplayName ',... 'Bisection - approx. error'); hold on; goid on; semilogy (linspace (1, length(et_Bisection), length(et_Bisection)), et_Bisection,... '..', 'Color', [228 26 28]./255, 'LineWidth', 1.5, 'DisplayName ,.... 'Bisection - true error'); semilogy (linspace(1, length(ea_FalsePos), length(ea_FalsePos)), ea_FalsePos, ... ' ', 'Color', [55 126 184 ]./255, 'LineWidth', 1.5, 'DisplayName , ... 'False-Pos - approx. error'); semilogy (linspace (1, length(et_FalsePos), length(et_FalsePos)), et_FalsePos,... '.', 'Color', [55 126184]./255,'LineWidth',1.5, 'DisplayName ,... 'False-Pos - tnue error'); semilogy (linspace(1, length (ea_ModFalsePos), length(ea_ModFalsePos)), ... ea ModFalsePos, ' ', 'Color', [lllll 175 74 ./255, 'Linewidth', 1.5, ... 'DisplayName', 'Mod False-Pos - approx. error'); semilogy (linspace(1, length(et_ModFalsePos), length(et_ModFalsePos)),... et ModFalseros, '..', 'Color', [77 175 74 ]. /255, 'LineWidth', 1.5, ... 'DisplayName , 'Mod. False-Pos - true error'); xlabel ('iteration', 'FontSize', I4,' Interpreter', 'latex'); ylabel ('abs. rel. error $(\%)$, 'FontSize , 14, 'Interpreter', 'latex'); legend ( 'Location', 'southeast', 'Fontsize', 12, 'Interpreter', 'latex'); function [p,h1,hu,hr,hfp]= initializePlotMFP (f,x1,xu,xr,f1,fu, methodstring ) figure; box on; hold on; grid on