Let A₁, A₂,... be a countably infinite collection of countably infinite sets, where A_i={a_i,1,a_i,2,a_i,3,...}. Consider the infinite array in which the first row is a_1,1,a_1,2,a_1,3,..., the second row is a_2,1,a_2,2,a_2,3,..., and in general the k-th row is a_k,1,a_k,2,a_k,3,...

(a) Explain why the array contains every element of 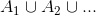. (In what cell of the array would one find the element a_ij?)

(b) Show how to construct a sequence that contains every element of the array.

(c) What does this tell you about 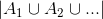? Why?

(d) Formally state the theorem that has been proved in this question.