Question: Let a and b be two complex numbers with b 0. Consider the function f(z) za bz - 1 defined on the set D

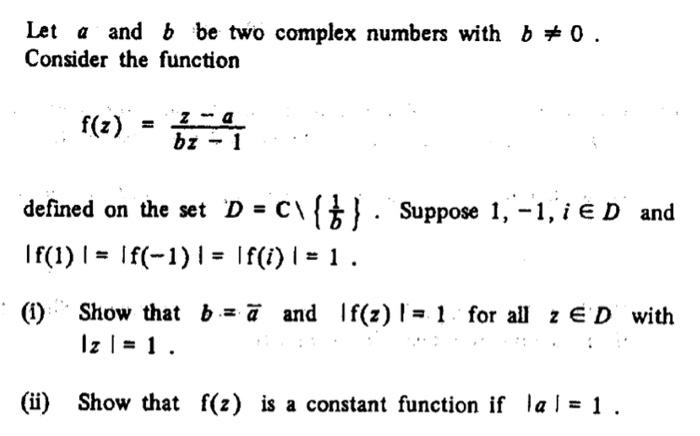
Let a and b be two complex numbers with b 0. Consider the function f(z) za bz - 1 defined on the set D = C\ {}. Suppose 1, -1, E D and |f(1) = f(-1) | = |f(i) | = 1. (1) Show that ba and f(z) = 1 for all z ED with Iz | = 1. (ii) Show that f(z) is a constant function if la = 1.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

i Suppose lzl1 Then we have 1fracfzf1 fraczalz1 cdot fraczbzbl fraczalz1 Plugging in z1 we get frac1... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let A and B be bounded nonempty subsets of R, and let A B : fa b : a 2 A; b 2 Bg. Prove that sup(A + B) = sup A + sup B and inf(A + B) = inf A + inf B.

Let A and B be n n matrices. According to Exercise 8.2.23, the matrix products A B and B A have the same eigenvalues. Do they have the same Jordan form?

Let A and B be events. a. Use probability notation to represent the conditional probability that event B occurs, given that event A has occurred. b. In part (a), which is the given event, A or B?

A feature of most autumns in the northeastern United States is a period of mild, sunny weather called Indian summer, which occurs when an anticyclone happens to stall for a few days off the East...

Northern Refineries does not avoid risk by selling oil futures. If prices stay above $1.60 a gallon, then it will actually have lost by selling oil futures at that price. Is this a fair comment?

Problem refer to the area A and perimeter P of a rectangle with length l and width w (see the figure). The perimeter of a rectangle is 160 m. Express the area A(w) as a function of the width w, and...

How does the literal nature of computers limit them? How have advances in computing enabled machine learning to remove these limitations?

At January 1, 2010, Cheng Company reported retained earnings of 20,000,000. In 2010, Cheng discovered that 2009 depreciation expense was understated by 4,000,000. In 2010, net income was 9,000,000...

Which of the following forms of compensation is most likely to align the interests of managers and shareholders? A compensation that is linked to company's employee friendiness A fixed compensation (...

What characteristics of a property, plant, and equipment item make it different from other assets, such as accounts receivable or inventory?

Mike Flannery holds the following portfolio: Stock Investment Beta A $150,000 1.40 B $10,000 0.80 C $140,000 1.00 D $75,000 1.20 What is the portfolio's beta? The beta of a portfolio is equal to the...

I am responsible for paying all the bills at my company. I notice that we, the buyers, have received a shipment for which the bill of lading says, "freight prepaid". Am I correct that we will be...

Situation Roles: You = Account Manager at Amazon Para = Marketing Director at Blue Intelligence, Inc. Taylor = Your manager at Amazon Background: In addition to concerns over higher costs during your...

How can job costs be misrepresented? a.) Recording cost information for cost control. b.) Stating the level of completion to show performance. c.) Charging costs to the wrong jobs. d.) Assigning...

What are the major considerations for initiating a logistics alliance? In implementation? In maintenance?

Edward Lee manufactures and sells homemade wine, and he wants to develop a standard cost per litre. The following are required for production of a 250-litre batch: 120.00 litres of grape concentrate...

Clifford uses a vehicle in his self-employment activity. In 2020, business use dropped to 40%. Self-employment activity dropped to 40% business use. In 2018, when he put the vehicle into service, he...

Baxter, Inc., owns 90 percent of Wisconsin, Inc., and 20 percent of Cleveland Company. Wisconsin, in turn, holds 60 percent of Clevelands outstanding stock. No excess amortization resulted from these...

Suppose that n = 5 observations are taken from the uniform pdf, fY (y; ) = 1/, 0 y , where is unknown. Two unbiased estimators for are 1 = 6/5Y max and 2 = 6Y min Which estimator would be...

The cdf for a random variable Y is defined by FY (y) = 0 for y 1. Find P (1/4 Y 3 4) by integrating fY (y).

Show that the common belief in the propensity of babies to choose an inconvenient hour for birth has a basis in observation. A maternity hospital reported that out of one years total of 2650 births,...

Alexander Corporation (a U.S.-based company) acquired 100 percent of a Swiss company for 8.2 million Swiss francs on December 20, Year 1. At the date of acquisition, the exchange rate was $0.70 per...

How does a parent company determine the appropriate method for translating the financial statements of a foreign subsidiary?

Gramado Company was created as a wholly owned subsidiary of Porto Alegre Corporation on January 1, Year 1. On that date, Porto Alegre invested $42,000 in Gramado's capital stock. Given the exchange...