Question: Let a, b, c E C, a = 0, and put h(z) = az + B, fc(z) = z2 + c. Define f=h-lo fcoh. Using
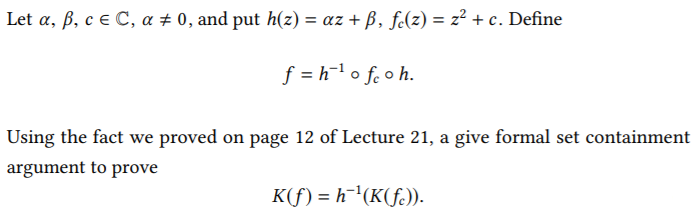

Let a, b, c E C, a = 0, and put h(z) = az + B, fc(z) = z2 + c. Define f=h-lo fcoh. Using the fact we proved on page 12 of Lecture 21, a give formal set containment argument to prove K(f) = h-'(K(f.)). we we can So need to know that solve the system a = x 2B = b, d = B+C-3 > Let
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


