Let be a simple graph as above, except that each edge is "oriented", meaning that edges are taken to be ordered pairs of vertices, where the first vertex is the "tail" and the second vertex is the "tip" of the edge, which we can draw as an arrow.

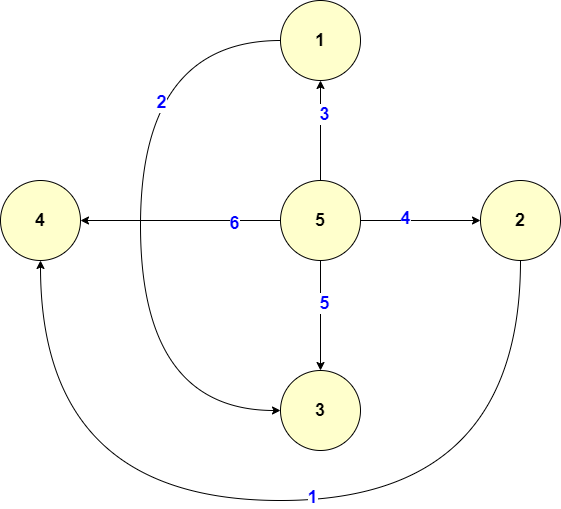
Let I be a simple graph as above, except that each edge is "oriented", meaning that edges are taken to be ordered pairs of vertices, where the first vertex is the "tail" and the second vertex is the "tip" of the edge, which we can draw as an arrow. In addition to labeling the vertices as before, let us also label the edges {1, 2, ..., m}. Then the fastening matrix Fs is the n x m matrix whose (i, j) entry is 0 if vertex i is not in edge j, but is 1 or -1 when edge j begins at v; or ends at vi, respectively. 1. Write the fastening matrix for the graph below. 2 3 4 5 5 4 2 5 3 2. Determine the rank of the fastening matrix in the above example. Formulate and prove a conjecture about what its rank should be for any oriented graph. 3. Consider edges 2, 3, 5: are the corresponding columns of Fr linearly independent? What about edges 1,4,6? What about edges 2,3,4? State a conjecture about when a list of edges should have linearly independent columns of Fr Let I be a simple graph as above, except that each edge is "oriented", meaning that edges are taken to be ordered pairs of vertices, where the first vertex is the "tail" and the second vertex is the "tip" of the edge, which we can draw as an arrow. In addition to labeling the vertices as before, let us also label the edges {1, 2, ..., m}. Then the fastening matrix Fs is the n x m matrix whose (i, j) entry is 0 if vertex i is not in edge j, but is 1 or -1 when edge j begins at v; or ends at vi, respectively. 1. Write the fastening matrix for the graph below. 2 3 4 5 5 4 2 5 3 2. Determine the rank of the fastening matrix in the above example. Formulate and prove a conjecture about what its rank should be for any oriented graph. 3. Consider edges 2, 3, 5: are the corresponding columns of Fr linearly independent? What about edges 1,4,6? What about edges 2,3,4? State a conjecture about when a list of edges should have linearly independent columns of Fr