Question: Let C Fn 2 be a non-empty binary code. Define the following quantities: R+(C) = max x2Fn 2 min c2C d(x, c), R(C) =

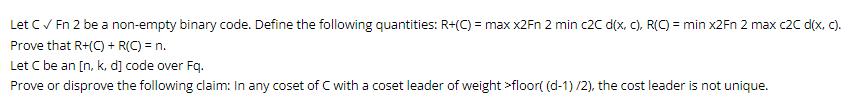
Let C Fn 2 be a non-empty binary code. Define the following quantities: R+(C)= max x2Fn 2 min c2C d(x, c),

Let C Fn 2 be a non-empty binary code. Define the following quantities: R+(C) = max x2Fn 2 min c2C d(x, c), R(C) = min x2Fn 2 max c2C d(x, c). Prove that R+(C) + R(C) = n. Let C be an [n, k, d] code over Fq. Prove or disprove the following claim: In any coset of C with a coset leader of weight >floor( (d-1)/2), the cost leader is not unique.

Step by Step Solution

★★★★★

3.50 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

A compare-exchange operation on two array elements A[i] and A[j], where i A[j] 2 exchange A[i] with A[j] After the compare-exchange operation,...

The following additional information is available for the Dr. Ivan and Irene Incisor family. The Incisors own a rental beach house in Hawaii. The beach house was rented for the full year during 2012...

2. Qualitative analysis studies require the use of a large number of chemical reagents, each of which must be treated with care. To illustrate this statement, list the reagents used to determine and...

hello I need help with my finance long discussion. Prompt: Discuss how you understand the following concepts instrumental in capital budgeting decision making: 1 Opportunity cost 2 Cannibalization 3...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

.QUESTION .all the questions to be thoroughly explained Invocations of its type operations involve no writes to persistent memory and no output to clients. Concurrent processes may invoke the object....

answer the question clearly (a) What is the von Neumann bottleneck and why can it limit performance on today's RISC machines? [4 marks] (b) What computer architecture techniques are used to mitigate...

You are required to develop a software that will let a user organize his or her music collection. Instead of a database you will be storing all the information in a file. Your program will be an...

1. What is the qualified immunity standard? (i.e. how does qualified immunity apply to government employees/workers) 2. How much immunity does the typical executive receive within the administrative...

Macmillan Learning The motion y(x, t) of a vibrating system is described by y(x,t) = Age at sin(kx - cot) where x denotes a distance in meters and denotes a time in seconds. Denoting units with...

A certain skincare company's profit in millions of dollars, P(t), can be modeled by the polynomial function P(t) = -2t +8t2 + 2t, where t represents the number of skincare items produced, in...

Complete the equation for the piecewise function graphed below. ao -7 -6 -5 -4 -3 -2 -1 { f(x) = { 6 + 5 4 { -2 -3 -4 {3 6 if 6 x 3 if 3

Create a function (could be piecewise) that demonstrates the following discontinuities. (a) jump discontinuity (b) point discontinuity (c) infinite discontinuity Prove that f(x) is continuous at x =...

e) Alice wishes to sign a document and send it to Bob using RSA signatures. Suppose she generates two primes p = 7, q = 11, and a public exponent e =43, and publishes (n. e) as her public key (6...

C mo responder a a la afirmaci n de que algunos de sus fabricantes por contrato producen mercanc a ilegal ( es decir, imitaciones de Gators ) que compiten con la marca?

Explain the term global capital markets. This chapter primarily discusses global equity markets. What other types of financial instruments are traded in these markets? How important are global...

Suppose that f is integrable on [0.5,2] and that for k = 0, 1,2. Compute the exact values of each of the following integrals. a) b) 2t f(x) dx = 0.5 xk f(x) dx + 2k2 = 3 + k2 1-x2) dx

Prove that if a

Prove that (1-cos( 1/k)| 2.

A $100,000, 168-day Government of Canada Treasury bill was purchased on its date of issue to yield 3.7%. a. What price did the investor pay? b. CalculatethemarketvalueoftheT-bill85days later if the...

If $3702.40 earned $212.45 interest from September 17, 2004, to March 11, 2005, what rate of interest was earned?

On a $10,000 principal investment, a bank offered interest rates of 3.45% on 270- to 364-day GICs and 3.15% on 180- to 269-day GICs. How much more will an investor earn from a 364-day GIC than from...