Let

D={d_(1),d_(2),d_(3)}

and

F={f_(1),f_(2),f_(3)}

be bases for a vector space

V

, and suppose

f_(1)=6d_(1)-d_(2)+2d_(3),f_(2)=5d_(2)+d_(3),f_(3)=-4d_(1)+2d_(3)

.\ a. Find the change-of-coordinates matrix from

F

to

D

.\ b. Find

[x]_(D)

for

x=f_(1)-4f_(2)+4f_(3)

.\ a.

P_(DlarrF)=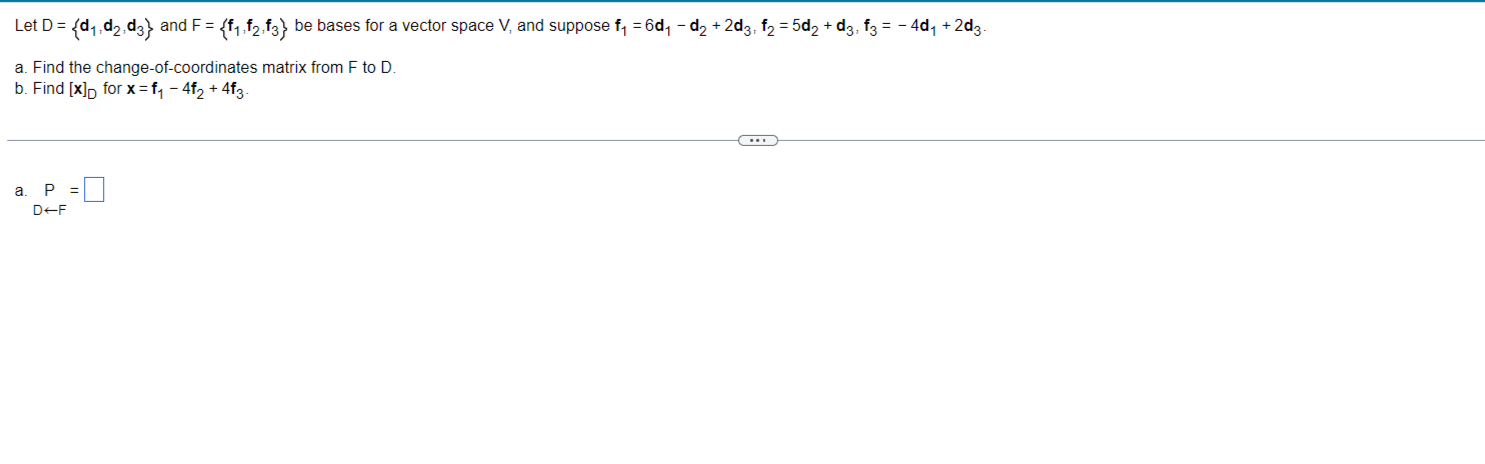

Let D={d1,d2,d3} and F={f1,f2,f3} be bases for a vector space V, and suppose f1=6d1d2+2d3,f2=5d2+d3,f3=4d1+2d3. a. Find the change-of-coordinates matrix from F to D. b. Find [x]D for x=f14f2+4f3. Let D={d1,d2,d3} and F={f1,f2,f3} be bases for a vector space V, and suppose f1=6d1d2+2d3,f2=5d2+d3,f3=4d1+2d3. a. Find the change-of-coordinates matrix from F to D. b. Find [x]D for x=f14f2+4f3