Question: Let f: [a, b] -> R be function. For r ER, we define following two subsets: U(I) = inf {f(y) | x 0} and An

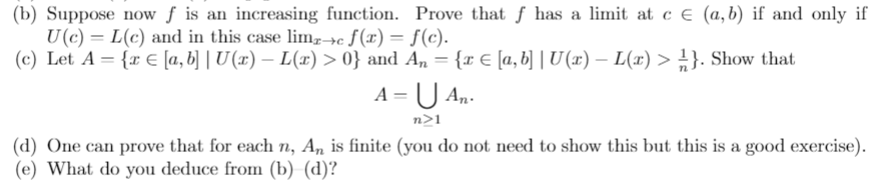
Let f: [a, b] -> R be function. For r ER, we define following two subsets: U(I) = inf {f(y) | x 0} and An = {r E [a, b] [ U(x) - L(x) > 1}. Show that A = U An. n>1 (d) One can prove that for each n, An is finite (you do not need to show this but this is a good exercise). (e) What do you deduce from (b) (d)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let f: [a, b] -> R be function. For r ER, we define following two subsets: U(I) = inf {f(y) | x

1. Read proposition 6.9 and answer the exercise after it. 2. Prove proposition 6.10(just prove the concave up). Proposition 6.10. Let f : (a, b) - R be conver or concave over (a, b). Then the...

1/ Can you help me to answer the exercise after proposition 6.9, please? 2/ Can you help me to prove proposition 6.10 (you may just prove concave up case), please? Proposition 6.10. Let f : (a, b) -...

Kindly show your steps pletely correct. 1. A production function is given by f(K. L) - L/2+VK. Given this form. MP - 1/2 and MPk - JR. (a) Are there constant returns to scale, decreasing returns to...

answer each part injective functions ( = one - to- one ) Let f: A -B be a function. 1. Complete the definition : f is called injective if Vas, aze A fla, ) = fraz ) = .. 2. Consider the function f:...

Part 1: We let f: A - B be a function. For any subset Y C B, we define the inverse image of Y under f (denoted by f-1(Y)) as the collection of elements in the domain A that maps to elements in f(Y)....

(i) Let f: A -> R be a function and B C A. Define g: B -> R as g(r) = f(x) for all r E B. Prove or disprove the following statement: The function f is uniformly continuous if and only if g is...

Introduction to analysis 12:37 (2) 3 of 3 prove it: if not, justify with an example. [ CO2, C5, 2.5 marks ] 2 Question 2 Let f : [a, b) - R be a bounded function. Suppose there exists a partition P...

1. [4 pt] Let f : A - B be a function. For any set C C A and D C B, we define . the image of C, denoted by f(C), to be the set f(C) = {y E B| there exists some r ( C s.t. y = f()}( ie., f (C) = {f(x)...

(13) (a) Let f : [a, b] - R be a continuous function. For x E (a, b) define [Df(x)], := MER |3(xn),=] C (x, b), such that lim Xn = x and lim f (x) - f(xn) = MS 11-+00 1-+00 x - Xn Prove that for any...

Initial capex investment of $1.5M at time zero, and $2.3M at time 1, as well as a ramping up of NWC of $0.9M immediately and and additional increase of $1.4M at time 1 (no more changes in NWC beyond...

Congratulations! Today is your 20 th birthday,but you are starting with nothing in the bank. You just startedworking full-time, earning $50,000 per year. Your goal is to have$5 million by your 60 th...

The grades of a class of 9 students on a midterm report (x) and on the final examination (y) are as follows: (a) Estimate the linear regression line. (b) Estimate the final examination grade of a...

According to the International Product Life Cycle Theory, the country(ies) most likely to manufacture a product that has been recently developed (one that is the result of a brand-new design and uses...

What is the main advantage to this tactic?

What administrative cost items are associated with this tactic?

What is the full-cost budget?