Let $f$ be a function defined on $[0,).$ Then the function $F$ defined by

$F(t)={\displaystyle \underset{0}{\overset{}{}}}{e}^{-it}gtdt$

Is sald to be the Laplace transferm of $f.$ The domain of $f(s)$ is the set of values of $s$ for which the gleen improper integral convergen.

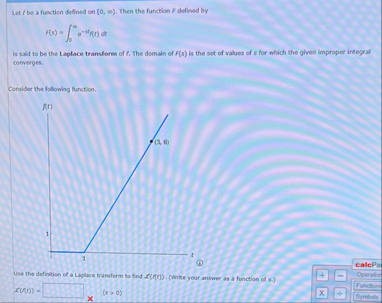
Consider the following function.

We the definition of a caplace tranform to find Let $f$ be a function defined on $[0,).$ Then the function $F$ defined by

$F(t)={\displaystyle \underset{0}{\overset{}{}}}{e}^{-it}gtdt$

Is sald to be the Laplace transferm of $f.$ The domain of $f(s)$ is the set of values of $s$ for which the gleen improper integral convergen.

Consider the following function.

We the definition of a caplace tranLet $f$ be a function defined on $[0,).$ Then the function $F$ defined by

$F(t)={\displaystyle \underset{0}{\overset{}{}}}{e}^{-it}gtdt$

Is sald to be the Laplace transferm of $f.$ The domain of $f(s)$ is the set of values of $s$ for which the gleen improper integral convergen.

Consider the following function.

We the definition of a caplace tranform to find Let $f$ be a function defined on $[0,).$ Then the function $F$ defined by

$F(t)={\displaystyle \underset{0}{\overset{}{}}}{e}^{-it}gtdt$

Is sald to be the Laplace transferm of $f.$ The domain of $f(s)$ is the set of values of $s$ for which the gleen improper integral convergen.

Consider the following function.

We the definition of a caplace tranform to find

Let $f$ be a function defined on $(0,m).$ Then the function $F$ defined by

$F(s)={\displaystyle \underset{0}{\overset{=}{}}}{e}^{-st}f(t)dt$

Is sild to be the Laplace transform of $f.$ The domain of $F(s)$ is the set of values of $s$ for which the given improper integral correrges.

Consider the following function.

calcPa

Use the definition of a Laplace branaform to find fit form to find