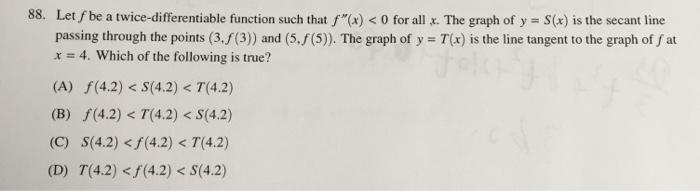
88. Let f be a twice-differentiable function such that f"(x) < 0 for all x. The graph of y = S(x) is the secant line passing through the points (3.f(3)) and (5,f(5)). The graph of y = T(x) is the line tangent to the graph of f at x = 4. Which of the following is true? (A) f(4.2) < S(4.2) < T(4.2) (B) f(4.2) < T(4.2) < S(4.2) (C) S(4.2)