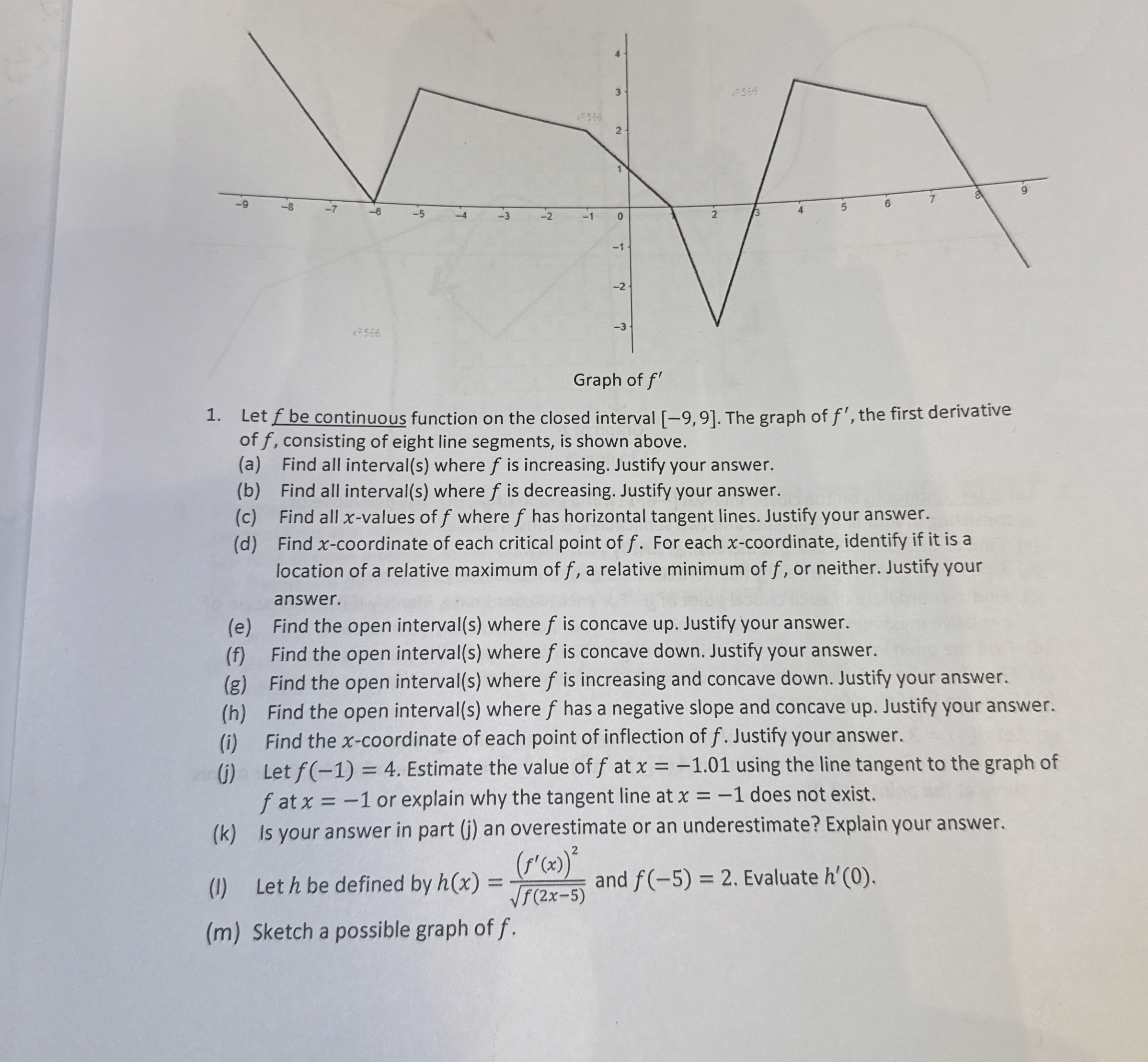
Let $f$ be continuous function on the closed interval $-9,9.$ The graph of $f^{\text{'}},$ the first derivative of $f,$ consisting of eight line segments, is shown above.

$($a$)$ Find all interval$($s$)$ where $f$ is increasing. Justify your answer.

$($b$)$ Find all interval$($s$)$ where $f$ is decreasing. Justify your answer.

$($c$)$ Find all $x-$values of $f$ where $f$ has horizontal tangent lines. Justify your answer.

$($d$)$ Find $x-$coordinate of each critical point of $f.$ For each $x-$coordinate, identify if it is a location of a relative maximum of $f,$ a relative minimum of $f,$ or neither. Justify your answer.

$($e$)$ Find the open interval$($s$)$ where $f$ is concave up$.$ Justify your answer.

$($f$)$ Find the open interval$($s$)$ where $f$ is concave down. Justify your answer.

$($g$)$ Find the open interval$($s$)$ where $f$ is increasing and concave down. Justify your answer.

$($h$)$ Find the open interval$($s$)$ where $f$ has a negative slope and concave up$.$ Justify your answer.

$($i$)$ Find the $x-$coordinate of each point of inflection of $f.$ Justify your answer.

$($j$)$ Let $f(-1)=4.$ Estimate the value of $f$ at $x=-1\mathrm{.}01$ using the line tangent to the graph of $f$ at $x=-1$ or explain why the tangent line at $x=-1$ does not exist.

$($k$)$ Is your answer in part $($j$)$ an overestimate or an underestimate? Explain your answer.

$($I$)$ Let $h$ be defined by $h(x)=\frac{(f^{\text{'}}(x){)}^2}{\sqrt[\phantom{2}]{f(2x-5)}}$ and $f(-5)=2.$ Evaluate $h^{\text{'}}(0).$

$(m)$ Sketch a possible graph of $f.$