Question: Let f: Rn R be a strongly convex differentiable function so that for some constant a > 0, it - - holds that (Vf(x)

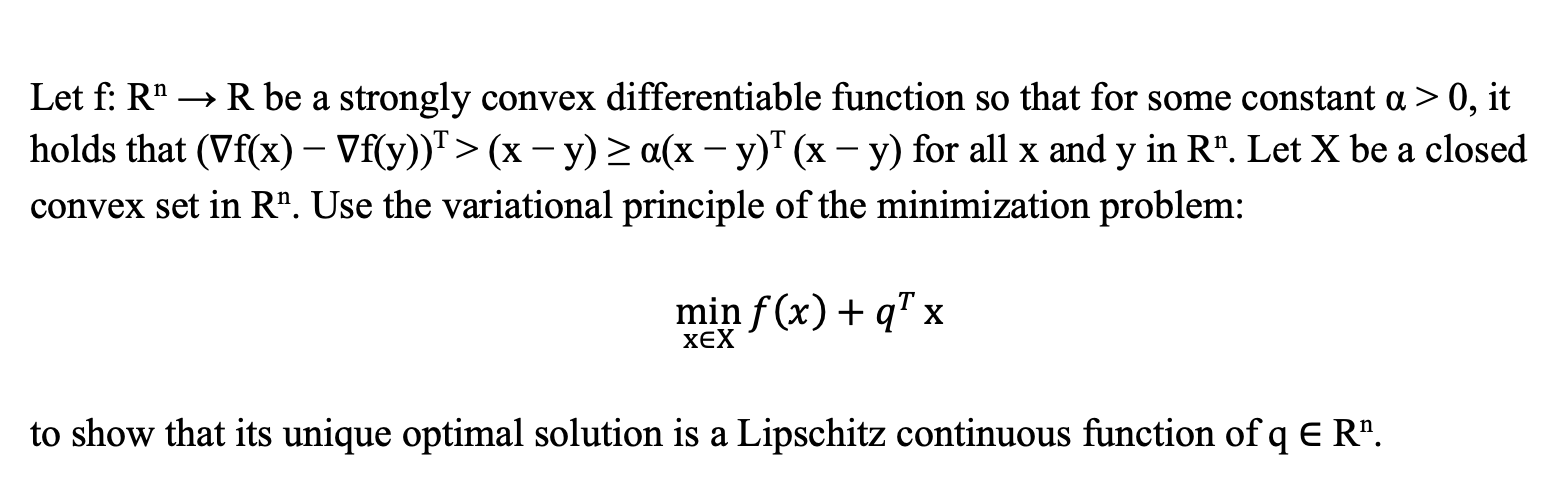
Let f: Rn R be a strongly convex differentiable function so that for some constant a > 0, it - - holds that (Vf(x) - Vf(y))>(x y) a(x y) (x y) for all x and y in R". Let X be a closed convex set in R. Use the variational principle of the minimization problem: minf (x)+q^ x XEX to show that its unique optimal solution is a Lipschitz continuous function of q = Rn.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Cicchetti Corporation uses customers served as its measure of activity. The following report compares the planning budget to the actual operating results for the month of December: Cicchetti...

The W-4 tax form is used to avoid paying income taxes on your paychecks. file your tax return. tell your employer how much federal income tax to withhold from your paychecks to send to the IRS....

References: Health Information Management Case Studies Second Edition AHIMA by Dianna M. Foley Health Information Management Technology an Applied Approah Sixth Edition AHIMA by Nanette Sayles and...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

a) Let f : Rn R be a convex function and let c R be a fixed number. Show that the set {x Rn | f (x) c} is a convex set. Hint: use the definitions of convex functions and convex sets. (b) Show that...

EE 127 / EE 227AT Homework Assignment #4 A Due date: 3/15/16 11AM. Please L TEX or scan your homework solution and submit the pdf on bCourses. Exercise 1 (A Boolean problem of maximal margin) We have...

Please answer questions a to e according to the following formula, and give detailed steps and explanations Recall that for a function f : RN - R, the gradient is simply the N x 1 vector formed by...

The materials used by the Hibiscus Company Division A are currently purchased from outside supplier at $54 per unit. Division B is able to supply Division A with 22,200 units at a variable cost of...

Kindly show your steps pletely correct. 1. A production function is given by f(K. L) - L/2+VK. Given this form. MP - 1/2 and MPk - JR. (a) Are there constant returns to scale, decreasing returns to...

Hi tutor. Kindly help me solve these I1 Exercise 2. Let f: R" + R be a real-valued function on R", and Xo = E R a In point. (a) If f is differentiable at Xo, explain what it means to say that the...

You are required to write regarding the use of spreadsheet software to analyze financial data and compute return and risk measures of financial securities in a complex environment. China Invest...

1. Discuss the impact of race, gender, and socioeconomic status on physical and psychological health. 2. In what ways does ones position in the class structure affect ones outlook, sense of...

In one month, you rent 2 new movies and 7 other movies from Option B . Would you have spent more or less with Option C ? Option A Rent premium movies for $ 1 8 . 9 9 / movie Rent nonpremium movies...

Determine the voltage transfer function and its magnitude characteristic for the network shown in fig 11.60 and identify the filter properties. C2 R2 R1 C1 V(t) Vot)

Bala learns that he has the beginnings of demyelination which will lead to multiple sclerosis. He knows that he has not paid the insurance premiums on his Term 20 policy. In review of his policy, he...

Write new versions of cons, car, and cdr that operate on streams. Using them, rewrite the code of the previous exercise to eliminate the calls to delay and force. Note that the stream version of cons...

Product placement is a form of advertising in which a companys products and name are intentionally positioned in motion pictures, television programs, radio broadcasts, and the like. Product...

Solve the given differential equation by undetermined coefficients. y'' + 2y' - 3y = 4e x - 9

6 Theory of Machines 5. A shaft carries five masses A, B, C, D and E which revolve at the same radius in planes which are equidistant from one another. The magnitude of the masses in planes A, C and...

A particle of mass m moves along the x-axis so that its position x and velocity v = dx/dt satisfy m(v2 - v20) = k(x20 - x2) where v0, x0, and k are constants. Show by implicit differentiation that m...

An object is taken from an oven at 300oF and left to cool in a room at 75oF. If the temperature fell to 200oF in hour, what will it be after 3 hours?

In Problems 1-4 draw the vector w. 1. w = u + 3 / 2 v 2. w = 2u - 3v 3. w = u1 + u2 + u3 4. w - u1 + u2 + u3

What are the ethical considerations involved in Harlows study? If you were on an ethics committee and Harlow presented his research proposal to you, would you approve it? What questions would you ask?

Based on the studies reviewed so far, would you say that attachment is predominantly biological, psychological or sociocultural? What are your arguments?

If you were to replicate a study using the Strange situation paradigm, what would you do to ensure that the study was conducted ethically? Think about the fact that you are creating distress in very...