Question: Let f RR be a function. Suppose a, b are two real numbers such that for any sequence (xi) with xia for all i

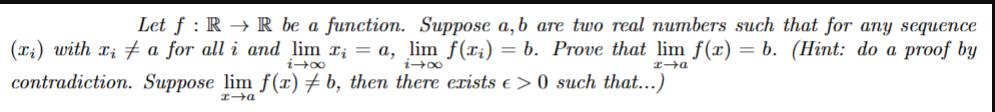
Let f RR be a function. Suppose a, b are two real

Let f RR be a function. Suppose a, b are two real numbers such that for any sequence (xi) with xia for all i and lim x = a, lim f(x) = b. Prove that lim f(x) = b. (Hint: do a proof by i4x x-a contradiction. Suppose lim f(x) #b, then there exists >0 such that...) xa

Step by Step Solution

★★★★★

3.39 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

If one attempted to dualize the notion of free module over a ring R (and called the object so defined "co-free") the definition would read: An R-module F is co-free on a set X if there exists a...

Let x1, x2, and x3 be distinct real numbers such that x1 (a) Show that T is a linear transformation. (b) Show that T is one-to-one. (c) Verify that if a1, a2, and a3 are any real numbers, then Where...

Let R be a ring with identity. Show that R is not a free module on any set in the category of all R-modules (as defined in Exercise 2). Data from in exercise 2 Let R be any ring (possibly without...

You are considering a project with an initial cash outlay of $71,000 and expected cash flows of $19,170 at the end of each year for six years. The discount rate for this project is 10.3 percent....

Hi y'all! If you could answer any of the questions here that would be AWESOME /tmp/282676-14774105227098708-32654-96170.dvi Express the function f(x) = x+8 x5 as a piecewise-defined function by...

Theorem 1 If lim f x L and lim f x M then L M x p x p Proof Suppose LM then I L MI 0 Since lim f x L if we take x p then 38 0 such that Ix pl 8 1 f x LI e Similarly since lim f x M 38 0 such that x p...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Could someone please check my work and let me know if I correctly used all of the included theorems that are referenced in the proof Please state all definitions and theorems that you will need:...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Recall that N is the set of positive integers and Q is the set of rational numbers. NOTE: "Limit point\Sequences - Part 2 (Week 4) Infinite Limits Definition. A sequence (sn) is said to diverge to +...

Shifters and Rotators. Shifters and rotators move bits andmultiply or divide by powers of 2. As the name implies, a shiftershifts a binary number left or right by a specified number ofpositions....

Question 4. (11 points) Assume that a closed economy is characterized by the following equations: Consumption: C = 100 + (2/3) (Y -T) Tax: T = 600 Government spending: G = 500 Investment: I = 800 -...

1.Suppose you have two part-time jobs, Restaurant Server and Uber Driver. After younger servers start working for less, employers pay only $11 instead of $14 per hour. What happens to your supply of...

Problem 1 - Brinell E Rockwell El Bookmark this page Test clue Jul 2?, 202212200 {33 Brinell 8. Rockwell D.Dl'2. points [gradedl Brinell s Rockwell lBaRl is a high-end manufacturer of cutting and...

What is the expected change in production volume, on average, as the number of factory workers decreases by five? Please enter the value of the expected change in production volume with ONE digit to...

The company has the following beginning balances in its stockholders\' equity accounts on January 1 , 2 0 2 4 : Common Stock, $ 1 0 0 , 0 0 0 ;Additional Paid - in Capital, $ 3 , 7 0 0 , 0 0 0 ; and...

t.com - Towel Help Save & Exit Submit Pro's Landing purchased $600 of office supplies on credit. The company policy is to initial record prepaid and unearned items in balance sheet accounts, WNch of...

Grace is training to be an airplane pilot and must complete five days of flying training in October with at least one day of rest between trainings. How many ways can Grace schedule her flying...

Construct functors as follows: (a) A covariant functor G S that assigns to each group the set of all its subgroups. (b) A covariant functor R R that assigns to each ring N the polynomial ring N[x]....

If G is a group, a, b G and bab -1 = a r for some r N, then b i ab -i = a i for all j N.

Proof that Let R be an integral domain with quotient field F. lf T is an integral domain such that R T F, then F is (isomorphic to) the quotient field of T.

Prepare a cause-and-effect diagram to analyze why a machine has produced a defective part.

Suppose you are going to have a prescription filled at a local pharmacy'. Referring to the dimensions of service quality, for each dimension, give an example of how you would judge tire quality' of...

Visit http://www.theacsi.org, select two companies that you are familiar with, and look up their customer satisfaction indices. Do the indices agree with your knowledge of the quality of the products...