Question: Let f: W W be defined as f(n) = n - 1, if n is odd and f(n) = n + 1, if n

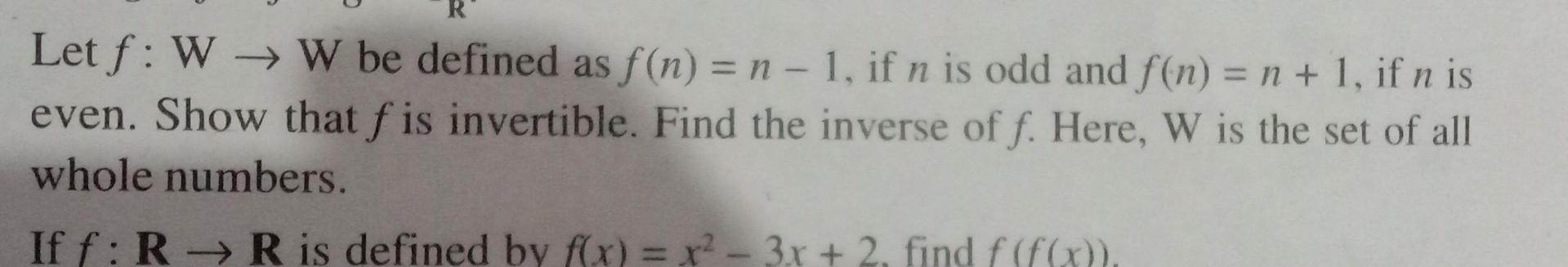
Let f: W W be defined as f(n) = n - 1,

Let f: W W be defined as f(n) = n - 1, if n is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers. If f: R R is defined by f(x) = x - 3x + 2, find f(f(x)).

Step by Step Solution

★★★★★

3.37 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

function fiWW defined by 5n1 if n is odd fn ntl if n is even i f ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

please answer blank boxes and those with red ex's beside them Ryan Ross (111-11-1112), Oscar Omega (222-22-2223), Clark Carey (333-33-3334), and Kim Kardigan (444-44-4445) are equal active members in...

Exercises 3150 contain rational equations with variables in denominators. For each equation, a. Write the value or values of the variable that make a denominator zero. These are the restrictions on...

The Fourier series of a signal x[n] and its coefficients X k are both periodic of the same value Nand as such can be written (a) To find the x[n], 0 ¤ n ¤ N 1, given X k , 0 ¤ k...

Corporate Venture Capital at Eli Lilly Read the case study and answer the following questions: What is the role of corporate venture capital? What is your assessment of Lilly Ventures? What should...

Marian Plunket owns her own business and is considering an investment. If she undertakes the? investment, it will pay $ 5 comma 440 at the end of each of the next 3 years. The opportunity requires an...

Let f be the function defined by f( n) = n^3 for each nN. For which of the following functions g is f( n) = O(g(n))? a) g(n) = n^2 + 1. b) g(n) = n^3 + 1. c) g(n) = 1/2 n^3 . d) g(n) = 1/2 n^4 . e)...

Let f be the function defined by f( n) = n^3 for each nN. For which of the following functions g is f( n) = O(g(n))? c) g(n) = 1/2 n^3 . d) g(n) = 1/2 n^4 . Just C and D please Let f be the function...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Question 16 (a-d only): Which of the following definitions describe functions from the domain to the codomain given? Which functions are one-to-one? Which functions are onto? Describe the inverse...

please help 5. Let n E N. Suppose that n is a perfect square that is n = m' for some m E Z. Show that 2n is not a perfect square. 6. Let f : Z - Z defined so that f(n) = -n + 3 if n is even and f(n)...

Discuss the impact that voice data entry could have on the accounting interface database forms.

3. Find the maximum likelihood estimates of the 2 x 1 mean vector u and the 2 x 2 covariance matrix E based on the random sample 3 6 4 4 X = 5 7 4 7 from a bivariate normal population. [5 + 12 marks]

find the length of the curve below on the given interval. y = ( x ^ 6 / 6 ) + ( 1 / 1 6 x ^ 4 ) on [ 1 , 3 ]

Prepare a Balance Sheet for Seafood Cuisine Inc. as of March 31, 2020 In January 2020, Mackenzie and Sophia Sidgman, co-owners of Seafood Cuisine got together to discuss the expansion of their...

Genuine Motor Products, located in Northern Ohio, manufactures precision measuring devices to monitor exhaust emission systems for new and used automobiles. Its products are sold worldwide.The firm...

Chase Company, an auto repair shop, established a $200 change fund on March 1. On March 2, the cash on hand at the end of the day was $856.75. Chase Company, an auto repair shop, established a $200...

What is the p-value of a test? Give a real-life example.

Burton Bush wants to retire in Arizona when he is 80 years of age. Burton, who is now 55, believes he will need $400,.000 to retire comfortably. To date, he has set aside no retirement money. If he...

What is the main purpose of a decisign support system?Help extract data and create executve-level reportsHeip interpret data and transiate it int 0- Hective decision makingHelp manage processes...

A causal LTI system has a transfer function (a) Find the poles and zeros of H(s), and from this determine if the filter is BIBO stable or not. (b) Draw a block diagram for such a system. (c) Find the...

A window is a signal w[n] that is used to highlight part of another signal. The windowing process consists in multiplying an input signal x[n] by the window signal w[n], so that the output is y[n] =...

When designing discrete filters the specifications can be given in the time domain. One can think of converting the frequency domain specifications into the time domain. Assume you wish to obtain a...

2. Identify the four major structures that compose a neuron.

20. What is a feature detectorpg78

10. Where does the optic nerve start and where does it endpg78