Question: Let f ( x , y ) be a differentiable function of two variables. Suppose at the point ( 1 , 1 ) fincreases most
Let be a differentiable function of two variables. Suppose at the point fincreases most rapidly in the direction of Also suppose that gradfgradf In addition, suppose that the level curve of passing by the point also passes by the point and that the tangent line to the level curve of f at also passes by the point Finally let. and
a Find and at the point Then estimate
b Find in direction of
c Find gradf
d Estimate
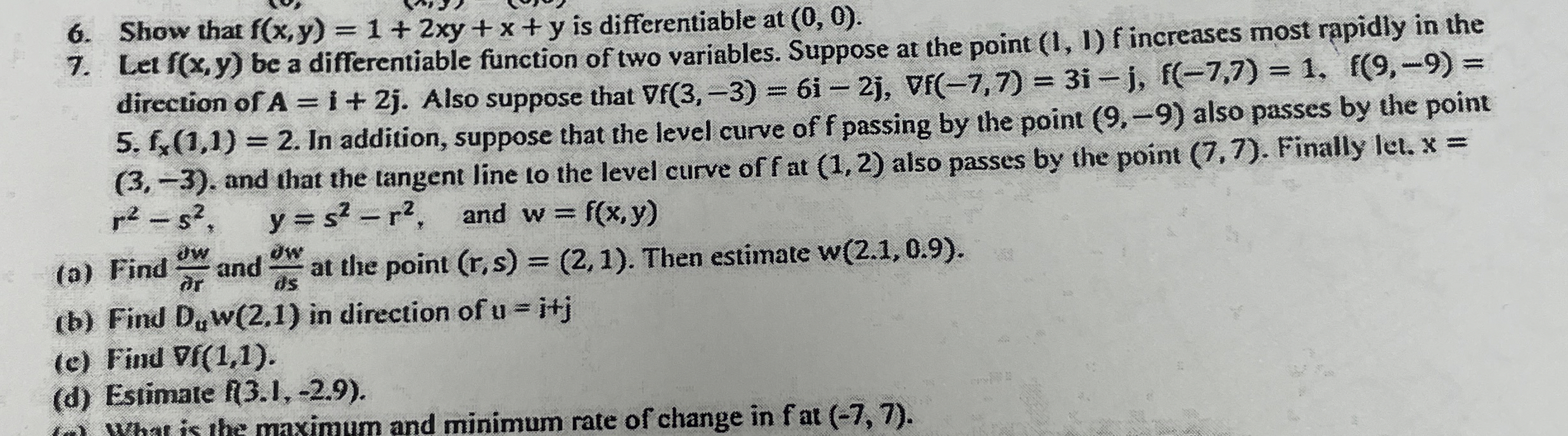
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


