Question: Let f(x) = 1 10 x50, g(x) = 5 log10 x + 35 Decide whether f = O(g) or g = O(f). Calculate the

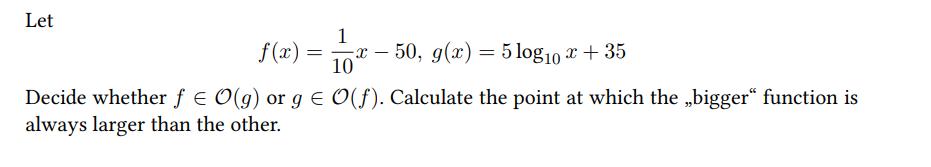
Let f(x) = 1 10 x50, g(x) = 5 log10 x + 35 Decide whether f = O(g) or g = O(f). Calculate the point at which

Let f(x) = 1 10 x50, g(x) = 5 log10 x + 35 Decide whether f = O(g) or g = O(f). Calculate the point at which the bigger function is always larger than the other. Let f(x) = 1 10 x50, g(x) = 5 log10 x + 35 Decide whether f = O(g) or g = O(f). Calculate the point at which the bigger function is always larger than the other.

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We will decide the comparison between fx and gx by determining their behavior as x tends to infinity ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Recall Exercise 6.2.37 on inhibitory control. Besides keeping track of the total time it took the animals to reach the food, the researchers also kept track of the amount of time the animals spent at...

Solve the equation: m +3 = m + 12

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Which of the following are the objective of financial statements? A. To provide information about economic resources and obligations of a business. B. To provide information about the earning...

UNIT 5 QZ, Q-20 UNIT 5 / UNIT 8 QUESTIONS KEEP ANSWERS SEPARATE BY UNITS UNIT II STUDY GUIDE Consumer Mathematics Reading Assignment See information below. Key Terms 1. Add-on interest method 2....

Part A Because you don't yet have an equation from your supervisor, choose one to help you set up the spreadsheet. Later, modify the spreadsheet when you receive the actual equation. Use spreadsheet...

Question 2 Find the asymptotes of the function. y = = x- 9 O Vertical asymptote at x = 9; horizontal asymptote at y = 1 O Vertical asymptote at x = -9; horizontal asymptote at y = 1 O Vertical...

Answer: Answer: 1'13 # 1 Let f (x) = 2(x + 3) and let g(x) be the # The function / (x) is an increasing inverse of f (x). Find g'(5). function about which little else is known other than f (2) = 7...

Purpose of This Assignment This assignment is intended to familiarize you with recursion. Because the functions and contracts in this assignment are the same as those assignment 2, the contract bonus...

BUSINESS CALCULUS INCOURSE TEST #1 (UNITS 1 & 2) SEMESTER 2 2022 SECTION A Instructions: Attempt ALL questions in this section. 1. Let f(x) be a function; what does it mean to say "f(x) has a limit...

Section 2.9: (page 148) Numbers 1, 2, 3, 4a, 6a Section 2.10: (page 154) Numbers 1-4 all Section 2.11: (page 159) Numbers 1-17 odd textbrokercom X 4." Final Exam X 6 1 Canvas LMS X e...

Draw the stereo isomers of these compounds: (a) 1, 3-Dimethyleyclohexane (b) 1, 2-Diethylcycloproane (c) 1-Chloro-3-methylcyclopentane

Business Decision Case New Haven Corporation recently identified an investment opportunity involving the purchase of a patent that will permit the company to modify its line of CD recorders. The...

In BOT projects, the concessionaire is designed to achieve theobjective of executing progress, monitor, and control processeswhile responding to all threats and opportunities using...

Let u(t) = 9ti+ (t - 9)j- 2k and v(t) = e'i+8 e j- e 8k. Compute the derivative of the following function. u(t) v(t) Select the correct choice below and fill in the answer box(es) to complete your...

On September 30, 2012, Sandhill Company issued 12% bonds with a par value of $620,000 due in 20 years. They were issued at 97 and were callable at 106 at any date after September 30, 2017. Because...

Your new client, Tinky, decided in 2019 that she was going to be a professional gambler. She lives in Dallas, spends Monday-Friday doing grunt work that she hates (but it pays the bills), and started...

Consumerism replaces the model of the consumer as someone who buys necessities in order to get on with their lives, with the model of the consumer as someone who buys in order to live. Can you put...

Performed brilliantly by the brand Nutter Butter on its social media ; zulurms, chaos marketing represents the latest attempt to stand out in acluticred, notsy marketplace. This radically innovative...

Please answer the following questions regarding the taxability of Social Security: a. A 68-year-old taxpayer has $20,000 in Social Security income and $100,000 in tax-free municipal bond income. Does...

Frederick (Freddy) Freeweights (age 42) owns and operates a health club called ''Treadmills West.'' The business is located at 4321 Arnold Street, Alpine, CA 91901. Freddy had the following income...

Carol Harris, Ph.D, CPA, is a single taxpayer and she lives at 674 Yankee Street, Durham, NC 27409. Her Social Security number is 793-52-4335. Carol is an Associate Professor of Accounting at a local...

4. Correlate brain anatomy with behavior. Do people with some unusual behavior also have unusual brains? If so, in what way?

19. What does fMRI measure?

23. Why do recent studies show a stronger relationship between brain size and IQ than older studies did?