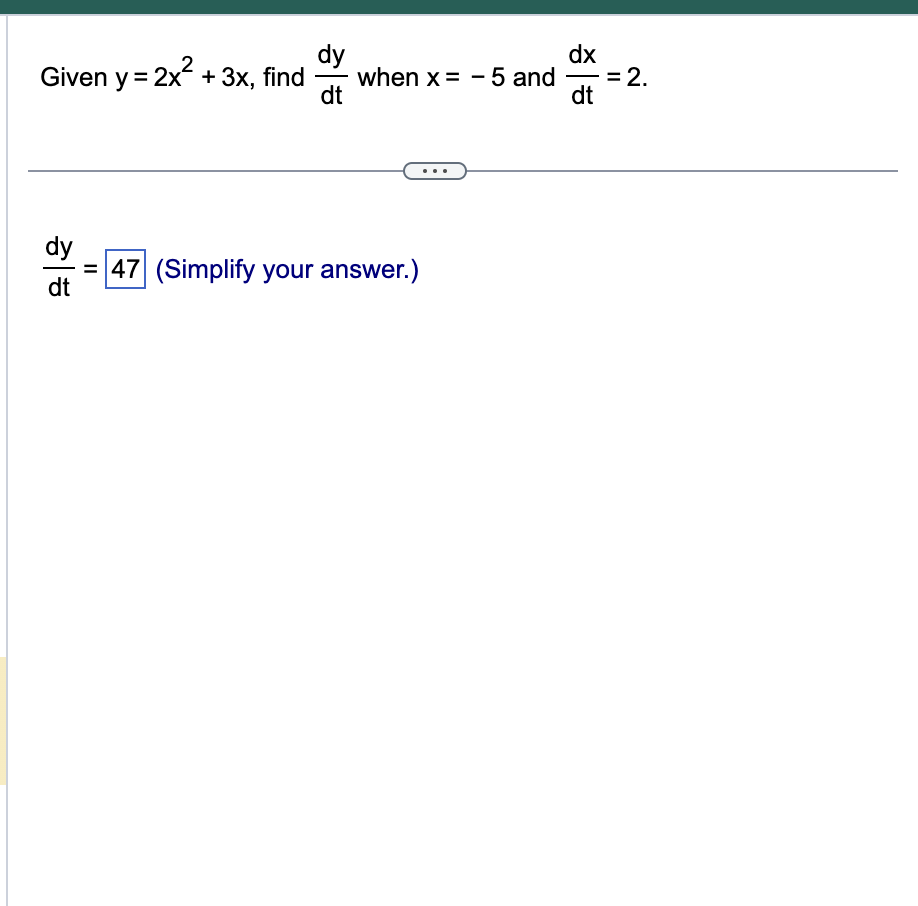
| Let f(x) = 7x. a) Find the linearization L(x) of fat a=>5. b) Use the linearization to approximate 7(5.1 )2. c) Find 7(5.1)2 using a calculator. d) What is the difference between the approximation and the actual value of 7(5.1)2. a) The linear approximation is L(x)=|70x - 175|. b) Using the linearization, 7(5.1)2 is approximately |182]. (Type an integer or a decimal.) c) Using a calculator, 7(5.1)2 is [{182.07|. (Type an integer or a decimal.) d) The difference between the approximation and the actual value of 7(5.1)% is 0.07|. (Type an integer or a decimal.) dy dx Given y = 2x + 3x, find dt when x = - 5 and =2. dt . . . dy 47 dt (Simplify your answer.)Find the absolute extrema of the function, if they exist, over the indicated interval. Also indicate the x-value at which each extremum occurs. If no interval is specified, use the real numbers, ( - co,co). f (x) = Vx; [0,64] . . . Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute maximum is 3 at x= 64 and the absolute minimum is 0 at x = ol (Use a comma to separate answers as needed.) O B. The absolute maximum is at X = and there is no absolute minimum. (Use a comma to separate answers as needed.) O C. The absolute minimum is at x = and there is no absolute maximum. (Use a comma to separate answers as needed.) O D. There is no absolute maximum and no absolute minimum