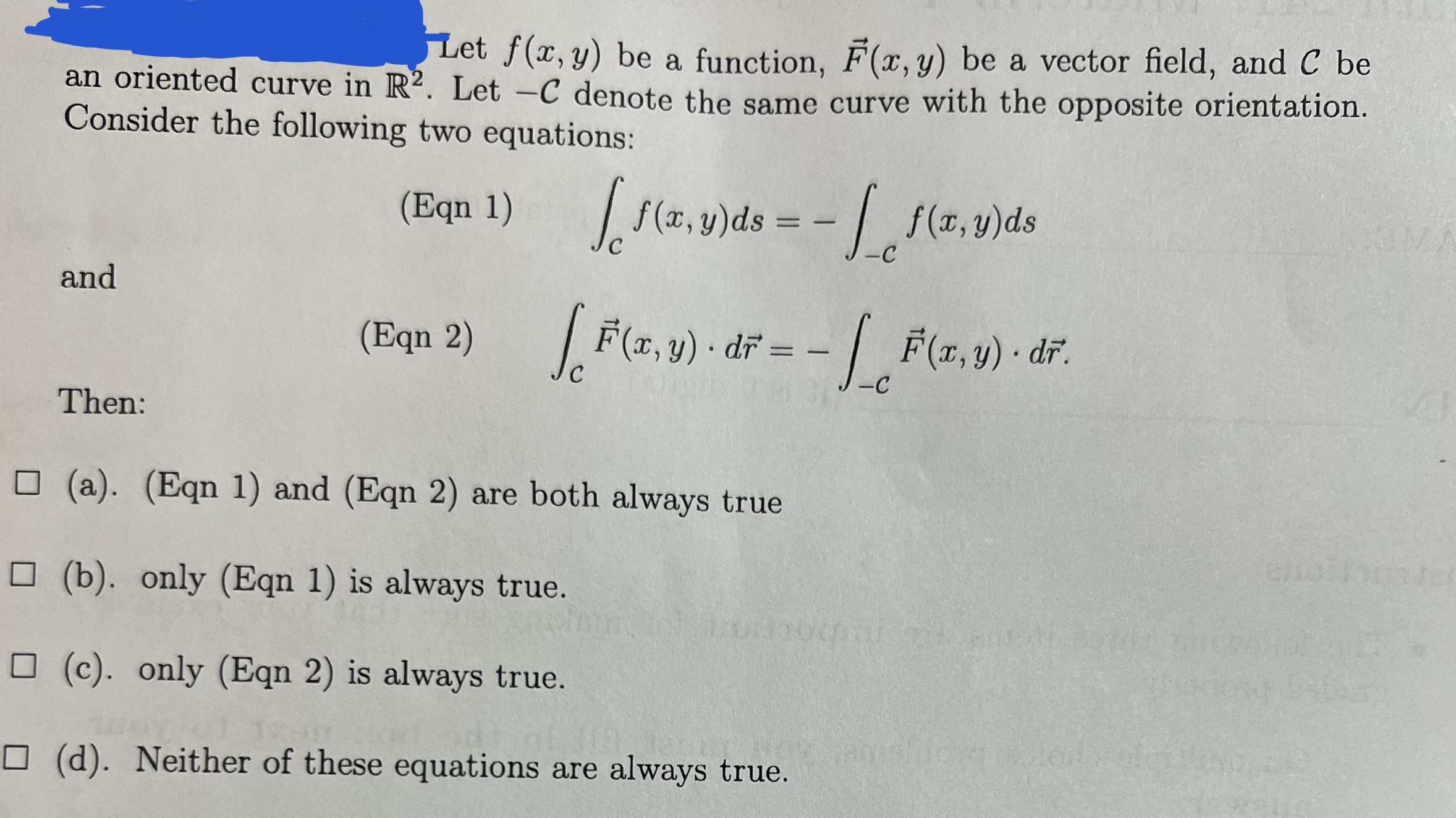
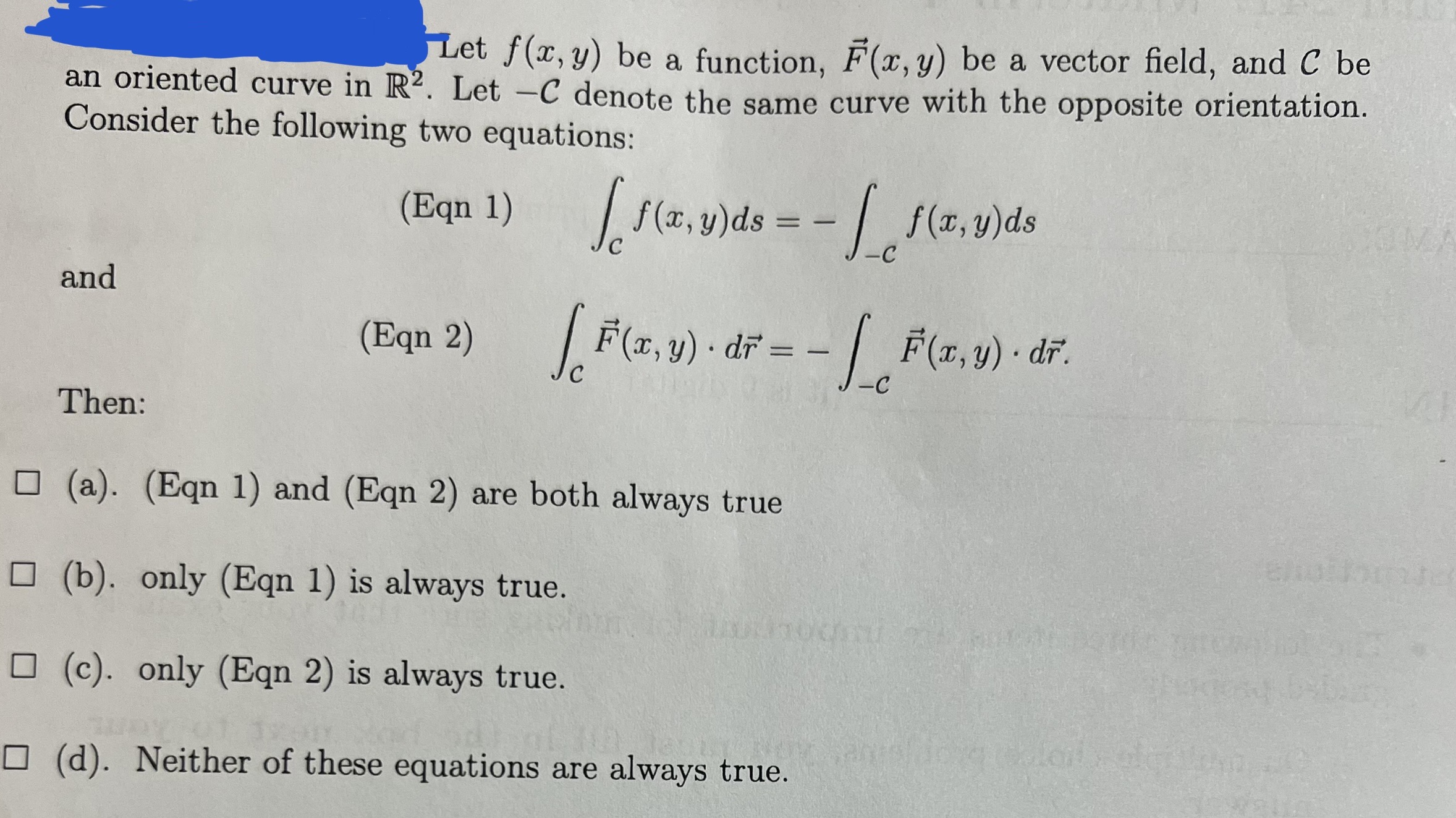
Let f(x, y) be a function, F(x, y) be a vector field, and C be an oriented curve in R2. Let -C denote the same curve with the opposite orientation. Consider the following two equations: (Eqn 1) f ( x, y) ds = - | f (x, y) ds and (Eqn 2) Jc F(x, y) . dr = - F(x, y) . dr . -C Then: (a). (Eqn 1) and (Eqn 2) are both always true (b). only (Eqn 1) is always true. O (c). only (Eqn 2) is always true. (d). Neither of these equations are always true