Question: Let G act on a non-empty set A. Prove that if a, b E A and b = g.a for some g = G,

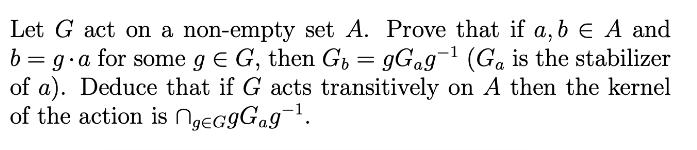
Let G act on a non-empty set A. Prove that if a, b E A and b = g.a for some g = G, then Gb = gGag- (Ga is the stabilizer of a). Deduce that if G acts transitively on A then the kernel of the action is ngeGgGag-.

Step by Step Solution

★★★★★

3.44 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Proof Let a and b be two elements in A such that b ga for some g G We need to show that G gGag First ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let G act on X via A. Show that for x, y EX that belong to the same orbit, there is a bijection between Stabe(a) and Stabc(y). (Hint: Use that x, y being in the same orbit means that there is czy E G...

For n Z+, n > 2, let f(x) Zn[x]. Prove that if a, b Z and a = b (mod n), then f(a) = f(b) (mod n).

Prove that if a; b R, then (a) -(a + b) = (-a) + (-b), (b) (-a) (-b) = a b, (c) 1/(-a) = -(1/a), (d) -(a/b) = (-a)/b if b 0.

In its first year of operation, Oriole Printing Shop estimated manufacturing overhead costs and activity in order to determine a predetermined overhead rate. At year end, March 31, overhead was...

The five independent projects shown below are under consideration for implementation by KNF Neuberger, Inc. The company's MARR is 15% per year. (a) Determine which projects should be undertaken on...

Donna has a checking account that charges $0.15 for each check written and a monthly service charge of $9.75. Write a formula that Donna can use each month to find the fees she will be charged....

Suppose that electrical shocks having random amplitudes occur at times distributed according to a Poisson process {N(t), t 0} with rate . Suppose that the amplitudes of the successive shocks are...

Clints Stonework Corporation was organized on January 1, 2013. For its first two years of operations, it reported the following: Required: On the basis of the data given, prepare a statement of...

A convenience store recently started to carry a new brand of soft drink. Management is interested in estimating future sales volume to determine whether it should continue to carry the new brand or...

The partners of Donald, Chief & Berry LLP decided to liquidate on August 1, 2019. The balance sheet of the partnership is as follows, with the profit and loss ratio of 25%, 45%, and 30%,...

Post by Day 4 a brief description of the three crisis-response organizations you selected. Then describe the roles of each organization as well as the relationships between and among them. Be...

A commercial building that has a value of $600,000 is insured on a Broad Perils policy with a coverage limit of $400,000. and a deductible of $1,000. 1. If a new building has a replacement cost of...

The reading and videos for this week bring to light some of the ethical and business-related issues in collecting and using data gathered about customer behaviors and using it to target advertising....

You are a large customer of a major Wall Street investment bank. They believe the price of oil will be going up over the next year and they are willing to enter an unlimited number of long positions...

Use the following diagram of TCP/IP protocols of a Network 1) Add the following servers to the network. a. DC server b. data server c. SMTP server d. Application server e.web server...

A recent article/publication (within the last five years) which showcases the use of molecular testing techniques to diagnose infectious diseases. The article may have a public health, clinical...

data table to plug in numbers in the balance sheet P2-3 (similar to) Balance sheet. From the following balance sheet accounts in the popup window, a. construct a balance sheet for 2016 and 2017. b....

B made an issue of 150,000 $1 ordinary shares at a premium of 20% the proceeds of which is received by cheque. What is the correct journal to record this? A. Bank Share capital Share premium B. Bank...

Let a, b, c Z+ with c = gcd(a, b). Prove that (ab)(c) = (a)(b)c.

Let G = S4, the symmetric group on four symbols, and let H be the subset of G where (a) Construct a table to show that H is an abelian subgroup of G. (b) How many left cosets of H are there in G? (c)...

(a) Find x in (Ug, ) where x 1, x 7 but x = x-1. (b) Find x in (U16, ) where x 1, x 15 but x = x-1. (c) Let k Z+, k 3. Find x in (U2k, ) where x 1, x 2k - 1 but x = x-1.

An auditor for Health Maintenance Services of Georgia reports 40% of policyholders 55 years or older submit a claim during the year. Fifteen policyholders are randomly selected for company records....

An internal study by the Technology Services department at Lahey Electronics revealed company employees receive an average of two non-work-related e-mails per hour. Assume the arrival of these...

Recent difficult economic times have caused an increase in the foreclosure rate of home mortgages. Statistics from the Penn Bank and Trust Company show their monthly foreclosure rate is now 1 loan...