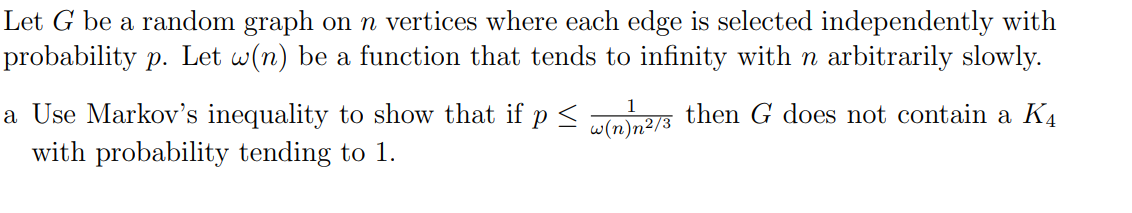
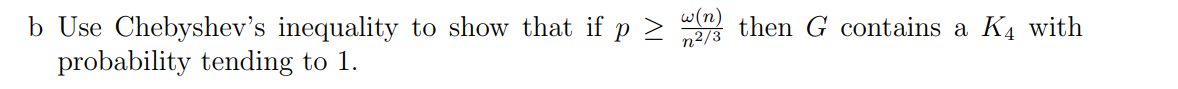
Let G be a random graph on n vertices where each edge is selected independently with probability p. Let w(n) be a function that tends to infinity with n arbitrarily slowly. a Use Markov's inequality to show that if p w(n)/3 then G does not contain a K with probability tending to 1. n2/3 b Use Chebyshev's inequality to show that if p (n) then G contains a K with probability tending to 1.