Question: Let g be continuous on an interval A and let F be the set of points where 9 fails to be one-to-one; that is,

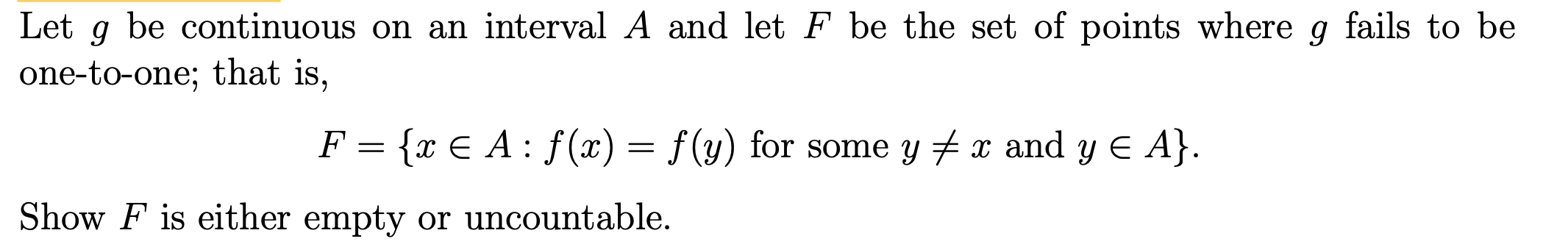
Let g be continuous on an interval A and let F be the set of points where 9 fails to be one-to-one; that is, F = {x A: f(x) = f(y) for some y + x and y = A}. Show F is either empty or uncountable.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show that F is either empty or uncountable we will use proof by contradiction A... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Give a detailed summary of the Fourth Amendment. In addtion explain how this amendment relates to the special needs doctrine? Explain wheat evidenc is. What are the types that can be used in trials?...

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...

Problems 113 122. The purpose of these problems is to keep the material fresh in your mind so that you are better prepared for later sections, a final exam, or subsequent courses such as calculus. X...

Show how periodic acid could be used to distinguish between an aldohexose and a ketohexose. What products would you obtain from each, and how many molar equivalents of HIO4 would be consumed?

What is the target market of the restaurant?

In what setting is the telepsychology being deliveredhome, clinic, school, public setting (library, caf, etc.), or somewhere else?

An investment offers a 14 percent total return over the coming year. Bill Bernanke thinks the total real return on this investment will be only 9 percent. What does Bill believe the inflation rate...

ABC Limited acquired the following assets in the respective years: - Kshs In year 2 0 2 0 In year 2 0 2 1 Generator . 2 , 0 0 0 , 0 0 0 Furniture and fittings. . 7 6 5 , 0 0 0 In year 2 0 2 2...

2. Firm ABC has based on nominal interest rate to compute and pay the interest payment because of its debt amount. Moreover, the firm has purchased an asset and use the Double Declining Balance Model...

The cylinder in the figure has a radius of 2 ft and rolls without slipping on the horizontal surface. The bar AB is attached to the periphery of the cylinder by a pin at point A. The other end of the...

A software company wants to improve its customer experience scores by 3% over the next 30 days. A data professional works to achieve this objective by understanding current scores and how far away...

ABC Insurance Company has a branch office, which consists of a branch manager and 5 clerical assistants. The branch manager reports to a division manager. The branch office has its own bank account...

A large tank of fish from a hatchery is being delivered to a lake. The hatchery claims that the mean length of fish in the tank is 15 inches, and the standard deviation is6inches. A random sample...

Emily Smith files her tax return on the basis of a fiscal year. Her records show that she received income in November 2021 and February 2022 from which there was backup withholding ($100 and $50,...

Tax Losses and Capital Losses Recouped The records of Gareth Young, an Australian resident, over three tax years disclosed: 2021/22 2022/23 2023/24 $ $ $ Assessable business income 54,000 72,000...

Need Help ASAP!! 6. Under a qualified profit-sharing plan, contributions must be made at least annually whether or not the employer has positive net income for the year True or False Defined-benefit...

Michelles trust is subject to 3.8% surtax on the lesser of the trusts net investment income or the excess of the trusts adjusted gross income over the $12,400 threshold (the highest trust tax rate)....

For each of the following functions, find its Taylor expansion centered at x0 = 1 and determine the largest interval on which it converges. a) ex b) log2(x5) c) x3 - x + 5 d) x

a) Prove that (x")' = nxn-1 for every n eN and every x e R. b) Prove that (xn")' = nxn-1 for every n -NU{0} and every x (0, ).

Suppose that x and y are extended real numbers and that {xn}, {yn}, and {wn} are real sequences. a) [SQUEEZE THEOREM FOR ]. If xn x and yn x, as n , and xn Answered: 1 week ago

Mary has just met an attractive man named Austin at a party. She wants to make sure she remembers his name. What should she do? a. Mary should chunk it by remembering the first three letters as a set...

Which neurotransmitter is no longer readily produced in Alzheimers patients? a. GABA b. dopamine c. endorphins d. acetylcholine

Which type of memory system best explains the What? phenomenon? a. echoic sensory system b. iconic sensory system c. short-term memory system d. tactile sensory system