Let $\frac{g}{L}=1\mathrm{.}00s^{-2},{}_0=\frac{}{6},$ and $dt=0\mathrm{.}005$ seconds. Graph the numerical approximation and the small angle approximation of the angle versus time on the same graph. Make sure the time interval is at least five cycles long.

Repeat Step $1$ for $dt=0\mathrm{.}01$ seconds and $dt=0\mathrm{.}1$ seconds. Of these three graphs, state which one is likely the most accurate depiction of reality and why.

Keep $dt=0\mathrm{.}005$ seconds. One separate graphs for the initial angles $($in radians$){}_0=0\mathrm{.}100,\frac{}{3},$ and. $\frac{}{2},$ graph the numerical approximation and the small angle approximation of the angle versus time on the same graph. Make sure the time interval is at least five cycles long. Describe how well the small angle approximation matches the numerical approximation as determined by initial angle. Be specific in how long it takes the two curves to deviate significantly.

Keep $dt=0\mathrm{.}005$ seconds. Let ${}_0=\frac{}{6}.$ One separate graphs for $\frac{g}{L}=2\mathrm{.}00s^{-2},0\mathrm{.}25s^{-2},$ graph the numerical approximation and the small angle approximation of the angle versus time on the same graph. Make sure the time interval is at least five cycles long. Describe the behavior and differences between the two approximations as you vary g$/$L$.$

Please turn in your answers to steps $2-4$ and all $8$ graphs. Please attach your computer code or spreadsheet

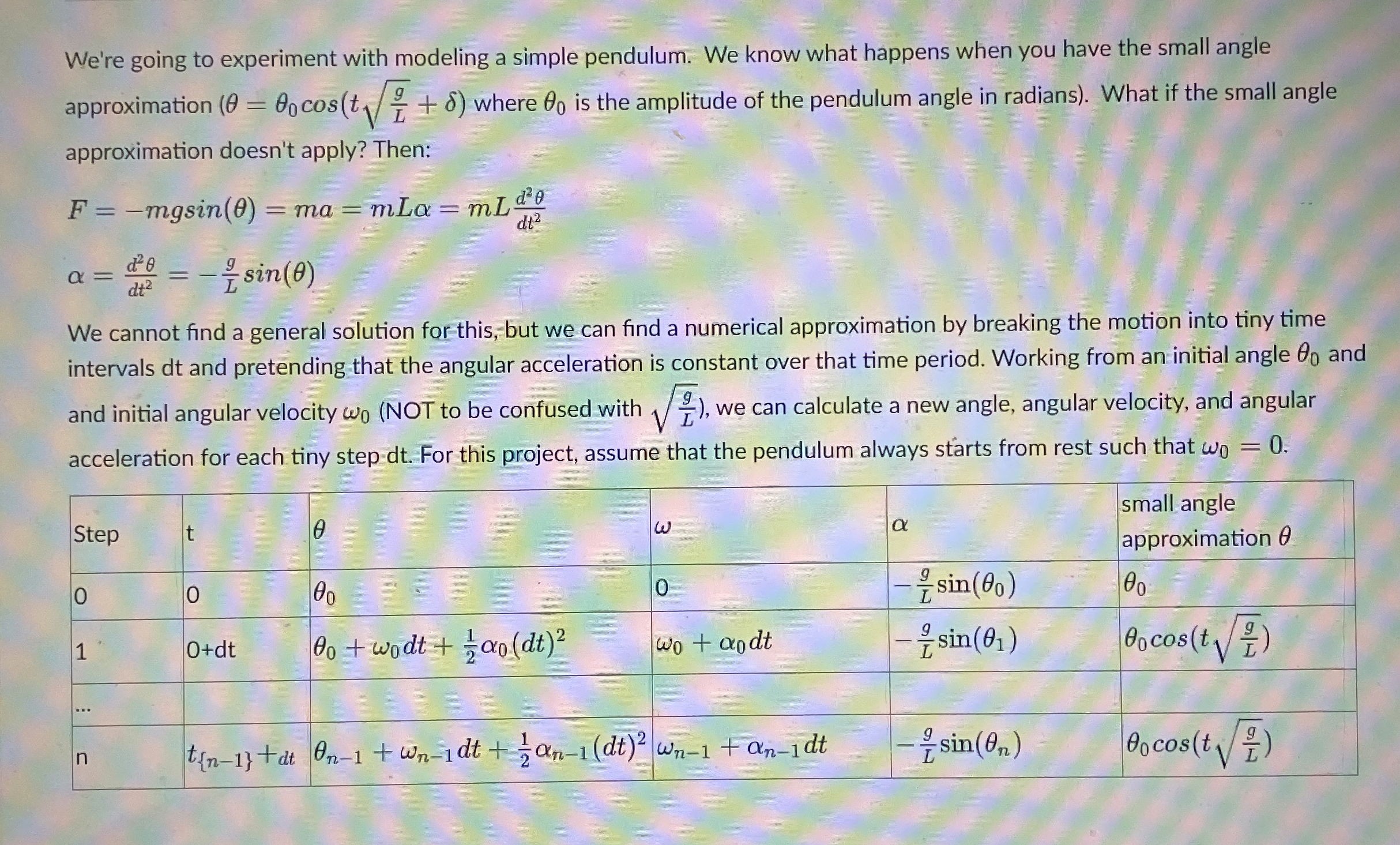
We're going to experiment with modeling a simple pendulum. We know what happens when you have the small angle approximation where ${}_0$ is the amplitude of the pendulum angle in radians$).$ What if the small angle approximation doesn't apply? Then:

$F=-$mgsin$()=ma=mL=mL\frac{d^2}{d{t}^2}$

$=\frac{d^2}{d{t}^2}=-\frac{g}{L}sin()$

We cannot find a general solution for this, but we can find a numerical approximation by breaking the motion into tiny time intervals dt and pretending that the angular acceleration is constant over that time period. Working from an initial angle ${}_0$ and and initial angular velocity ${}_0($NOT to be confused with $\sqrt[\phantom{2}]{\frac{g}{L}}),$ we can calculate a new angle, angular velocity, and angular acceleration for each tiny step dt $.$ For this project, assume that the pendulum always starts from rest such that ${}_0=0.$

$\backslash$table$[[$Step$,$t$,,,,\backslash$table$[[$small angle$],[$approximation $$