Question: Let $g: mathbb{Z} times mathbb{N} ightarrow mathbb{Q}$ be the function defined by $$ g(p, q)=frac{p}{q} $$ for all $(p, q) in mathbb{Z} times mathbb{N}$. Is
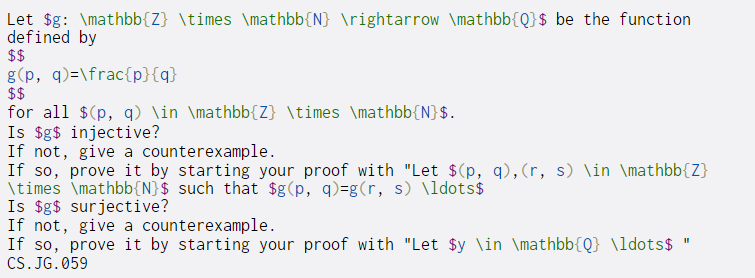
Let $g: \mathbb{Z} \times \mathbb{N} ightarrow \mathbb{Q}$ be the function defined by $$ g(p, q)=\frac{p}{q} $$ for all $(p, q) \in \mathbb{Z} \times \mathbb{N}$. Is $g$ injective? If not, give a counterexample. If so, prove it by starting your proof with "Let $(p, q),(r, s) \in \mathbb{Z} \times \mathbb{N} $ such that $g(p, q)=g(r, s) \ldots$ Is $g$ surjective? If not, give a counterexample. If so, prove it by starting your proof with "Let $y \in \mathbb{Q} \ldots$ CS. JG. 059
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


