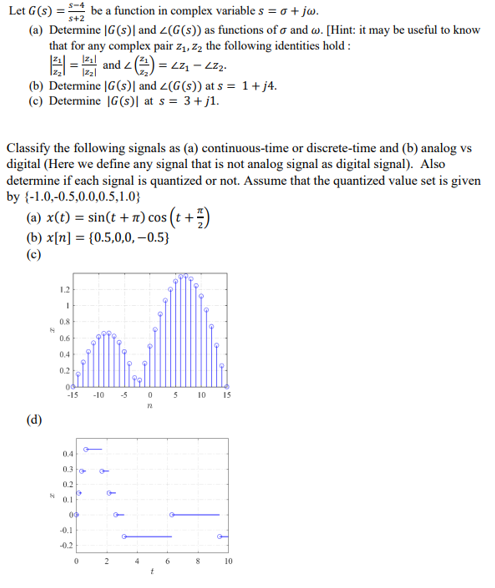
Let G (s) = = be a function in complex variable s = o + jw. $+2 (a) Determine |G(s) | and Z(G(s)) as functions of o and w. [Hint: it may be useful to know that for any complex pair Z1. Z2 the following identities hold : 1241 = 124 and 2 () = 421 - 272. (b) Determine |G(s)| and Z(G(s)) at s = 1+j4. (c) Determine |G(s)| at s = 3+ /1. Classify the following signals as (a) continuous-time or discrete-time and (b) analog vs digital (Here we define any signal that is not analog signal as digital signal). Also determine if each signal is quantized or not. Assume that the quantized value set is given by {-1.0,-0.5,0.0,0.5,1.0} (a) x(t) = sin(t + n) cos (t + =) (b) x[n] = (0.5,0,0, -0.5) (c) 1.2 0.6 0.4 0.2 -15 -10 -5 5 10 15 (d) 0.2 2 10