Question: = Let G = (V,E) be a directed graph with non-negative edge costs cle). Let se V be a starting node for shortest paths. Prove

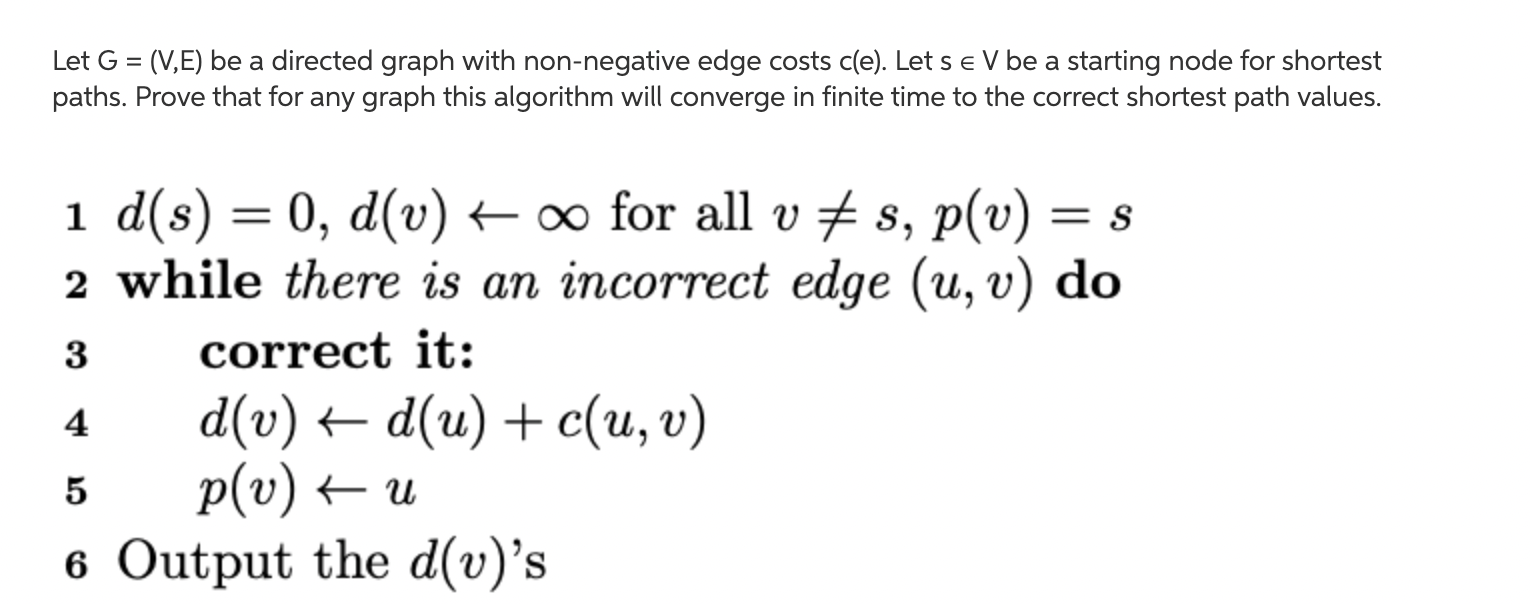
= Let G = (V,E) be a directed graph with non-negative

= Let G = (V,E) be a directed graph with non-negative edge costs cle). Let se V be a starting node for shortest paths. Prove that for any graph this algorithm will converge in finite time to the correct shortest path values. = = 3 i d(s) = 0, d(v) * oo for all v #s, p(v) = s 2 while there is an incorrect edge (u, v) do correct it: 4 d(v) + d(u) + c(u, v) p(v) + u 6 Output the d(v)'s 5

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

== As we talked in class, a program with two integer variables are universal. Now, we consider a spcial form of two variable programs. Let G = (V, E) be a directed graph, where V is a finite set of...

== 5. (A research problem, but I know the answer. 15pt) As we talked in class, a program with two integer variables are universal. Now, we consider a spcial form of two variable programs. Let G = (V,...

Let G (V,E) be a connected directed graph with non-negative edge lengths, let s and t be vertices of G. Suppose you computed the shortest path distances and a shortest path tree T from s using...

Prove Lemma 1 Definition 1 Let g = (V. E) be a directed graph, and let rooted, directed, spanning tree (RDST) o g is a subgraph T hold: V be a distinguished node that we call the root. A (V. E ) o g...

3 Max-Flow and Graph Reliability (35 pts] Let G = (V, E) be a directed graph with two specified vertices st EV. Assume that contains at least one s-t path. A subset of edges E' CE is a separating...

Q)a)(T/F) Let G = (V, E) be a directed graph with arbitrary (possibly negative) edge weights. Suppose, s,t ? V are two distinct vertices in G such that all directed paths from s to t in G contain no...

Let G = (V. E) be an undirected graph with all edge weights equal to I. Let d(i, j) denote the length of the shortest path between i and j. Now, suppose we wish to answer queries from the user of the...

How do I solve the second part, Alternating paths redux, using Dijkstra's algorithm. Please note that G is not acyclic. Alternating paths. Let G- (V, E) be a directed graph. Suppose every node u has...

Let G = (V, E) be a directed graph. We say that a set of paths are non-overlapping if they have no edges in common. For example, the set of 3 (purple, orange, and green) paths in the graph below form...

You plan on working for the next 35 years and don't think Social Security will be there. If you think you'll need $1,500,000 when you retire to fund your lifestyle, how much do you need to invest...

1. Consider the following embedded systems: a pager, a computer printer, and an automobile cruise controller. Create a table with each example as a column, and each row one of the following design...

BE13.2 (LO 1) (Classify activities.) Classify each of the transactions listed in BE13.1 as an operating (O), investing (I), financing (F), or significant noncash investing and financing (NC) activity...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

Question How can an executive determine whether it is better to defer compensation and pay the taxes later or to receive the compensation currently and pay taxes at relatively low income tax rates?

Question Can a corporation provide a nonqualified deferred compensation plan to an executive who is a controlling shareholder (more than 50%) in the corporation?

Question How can a governmental or tax-exempt employer provide a substantial deferred compensation benefit for an executive or key employee for whom the annual dollar limit would be inadequate?