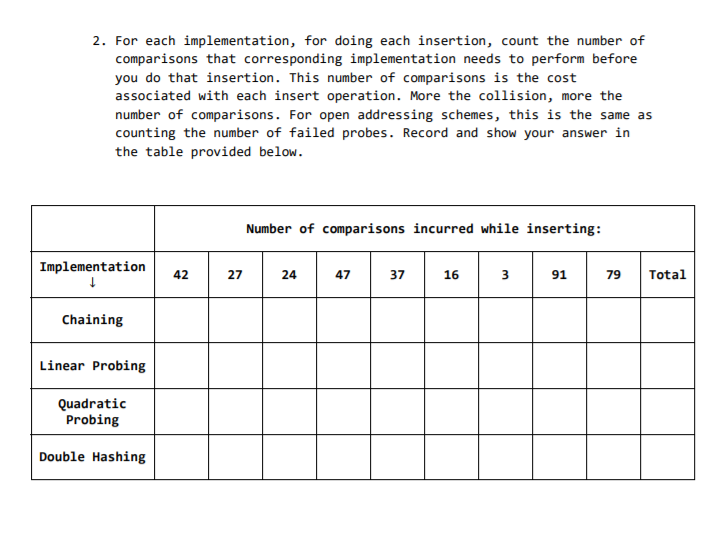
Let 'M' denote the hash table size. Consider the following four different hash table implementations: a. Implementation (I) uses chaining, and the hash function is hash(x)x mod M b. Implementation (II) uses open addressing by Linear probing, and the hash function is hi(x) = (hash(x) + f(i)) mod M, where hash(x) x mod M, and f(i)- c. Implementation (III) uses open addressing by quadratic probing, and the hash function is hx) (hash(x) + f(i)) mod M, where hash(x) -x mod M and f(i)-i. d. Implementation (IV) uses open addressing by double hashing, and the main hash function is hi(x) -(hash(x) + f (i)) mod M, where hash(X) = x mod M, and f(i) = x hash(x), and hash,(x) = 13- (x mod 7) Starting with an initially empty hash table of size 'M' for each of the above four implementations, INSERT the keys {42, 27, 24, 47, 37, 16, 3, 91, 79} (irn this specified order). While doing these insertions assume that the table size 'M' is kept fixed at '11' throughout (i.e., the code never calls the rehash function)