Let m, n ≥ 1. Show that for matrix A ∈ Rn×n, U ∈ Rn×m, C ∈ Rm×m, V ∈ Rm×n,

(Sherman–Morrison–Woodbury). Hint: Continue the following:

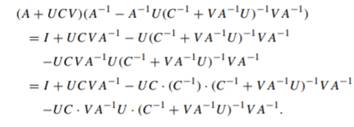
Let S be a subset of {1,...,N} and write the matrices X ∈ R(N−r)×(p+1) that consist of the rows in S and the rows not in S as XS ∈ Rr×(p+1) and X−S ∈ R(N−r)×(p+1) , respectively, where r is the number of elements in S. Similarly, we divide y ∈ RN into yS and y−S.

(a) Show

where HS := XS(XT X)−1XT S is the matrix that consists of the rows and columns in S of H = X(XT X)−1XT . Hint: Apply n = p + 1, m = r, A = XT X, C = I , U = XT S , V = −XS to (4.3).

(b) For eS := yS − ˆyS with yˆS = XSβˆ, show the equation’

Hint: From

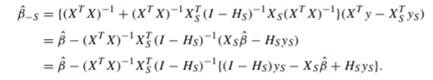
(A+UCV) =A-AU(C+VAU) VA-