Question: Let M = ( , Q, , q 0 , F ) be any DFA, and M 0 = ( , Q, , q 0

Let M = (, Q, , q₀, F) be any DFA, and M⁰ = (, Q, , q₀, Q \ F), quasi, M⁰ is the same as M except that the final states are non-final states and vice-versa.

Is the following true: 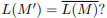Let M = (, Q, , q0, F) be any DFA, and Prove it.

L(M') = L(M)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Let M = (Q, , (delta), q0, F) = DFA and define CFG G = (V, , R, S) as follows: 1. V = Q; 2. For each q in Q and a in ,define rule q aq' where q' = delta(q, a); 3. For q in F define rule q ; 4. S =...

Let (140, q, q2}, {0, 1}, , o 192 be an NFA with given by the following table: 0 (a) Draw the state diagram of N. (b) Use the subset construction to construct an equivalent DFA M. Draw the state...

question in the picture For each of the following statements decide whether it is TRUE or FALSE. Justify your answer briefly. (a) Let g : Q \\ {0} > 0 \\ {0} be defined by g(a/b) = b/a. Then g is...

Please program in java Program-2 DFA State Minimization Backgrounds Deterministic State Acceptors play many important roles in computing applications such as compiler design and regular language...

Problem 2. Let M = (Q, 2, 8, 90, F) be a DFA and consider the DFA M' = (Q, 2, 8, 90, Q \F). Is it always true that L(M') = L(M) = * \ L(M)? What if one took a NFA N = (0,2, 8,90,F) and built a NFA N'...

Problem 6 (20 points). Let A = (Q, 9, 8, 90, F) be a DFA, where there exists a character ae that for all q e Q we have (q, a) = q, i.e. every state in A has a back-edge (loop back) for a. such a....

this is a computer science question Problem 6 (20 points). Let A = (Q, 9, 8, 90, F) be a DFA, where there exists a character ae that for all q e Q we have (q, a) = q, i.e. every state in A has a...

Could you explain each steps? 3. (a) Give the set up and construction steps of a proof that shows that the class of regular languages over an alphabet & is closed under the operation...

Definitions Suppose M = (Q, , , q0, F) is a DFA, as defined by Sipser. Given state p Q and input string x , let (p, x) denote the state that we reach, if we start in state p and then read string x....

2. Consider an arbitrary DFA M = (Q, {0,1), ?, 40, F) and call the language of this DFA L. Fill in the blanks in the definition of a new DFA whose language is the result of taking each string in L...

The makers of Tylenol pain reliever do a lot of advertising and have loyal customers. In contrast, the makers of generic acetaminophen do no advertising, and their customers shop only for the lowest...

KIA Corporation, commonly known as KIA is a South Korean Multinational Automobile manufacturer. With its headquarters in Seoul, South Korea, it is the second largest automobile manufacturer of South...

Sandra and Kelsey are forming a partnership. Sandra will invest a piece of equipment with a book value of $ 4 , 8 0 0 and a fair market value of $ 1 3 , 1 0 0 . Kelsey will invest a building with a...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

5. If yes, then why?

3. What changes should I be making?

1. I dream of being so good at what I do that my expert advice will be sought continually.