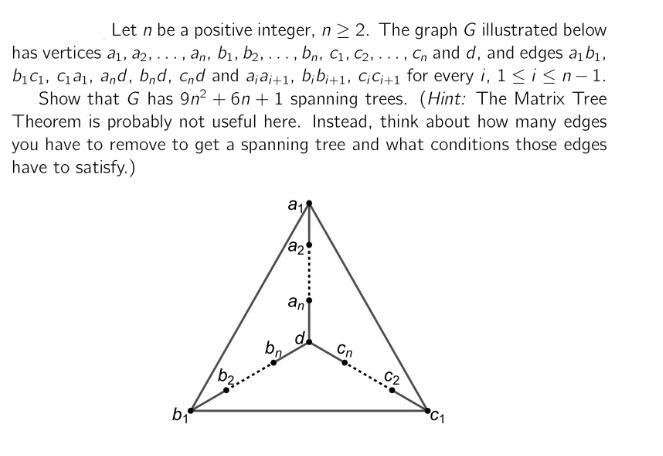
Let n be a positive integer, n2. The graph G illustrated below has vertices a1, a2, ..., an, b1, b2, ..., bn. C1, C2, ..., C, and d, and edges ab, bici, cia, and, bnd, cnd and aja+1, bibi+1, CiCi+1 for every i, 1in-1. Show that G has 9n2 + 6n+1 spanning trees. (Hint: The Matrix Tree Theorem is probably not useful here. Instead, think about how many edges you have to remove to get a spanning tree and what conditions those edges have to satisfy.) b b2. a a2 an d bn 02 C