Question: Let N = min{n|Sn 5 B or 3.; 2 A}, where A is a positive integer, B is a negative integer, and S = X1+Xg+...+X,..

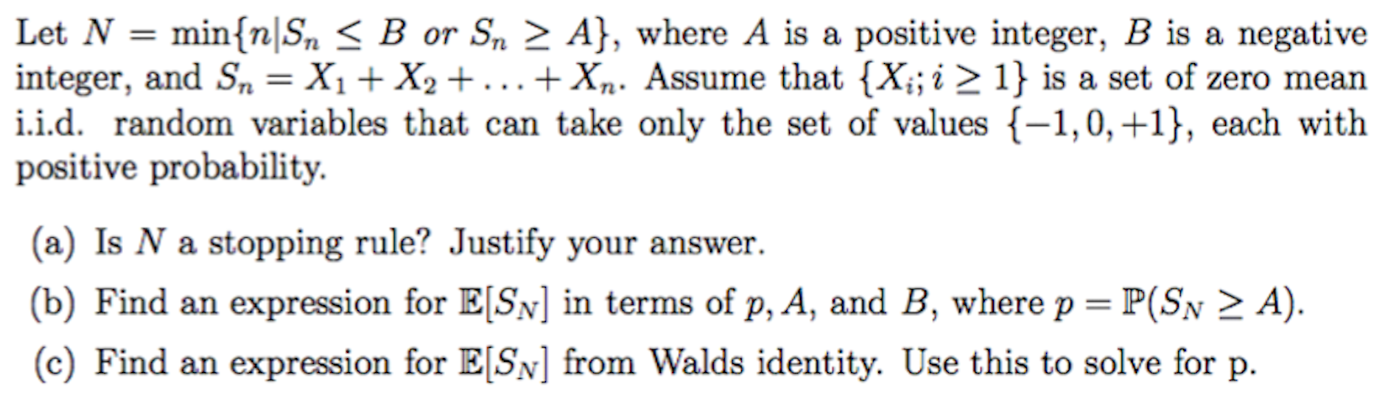
Let N = min{n|Sn 5 B or 3.; 2 A}, where A is a positive integer, B is a negative integer, and S" = X1+Xg+...+X,.. Assume that {X5122 1} is asst ofzero mean i.i.d. random variables that can take only the set of values {1,0, +1}, each with positive probability. (a) Is N a stopping rule? Justify your answer. (b) Find an expression for E[SN] in terms of p, A, and B, where p = 1P(SN 2 A). (c) Find an expression for E[SN] from Walds identity. Use this to solve for p

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

All the information is in the question. 2 (a) Let {Yt} be a weakly stationary process and let X, = B'l'}, where B is the backshift operator and r is a positive integer. Do {K} and {Xi} have the same...

MATH:4050: Introduction to Discrete Mathematics. Homework 6 due 10/06/17. 1. Find the coecient of x41 x22 x3 in the expansion of (2x1 6x2 8x3 )7 . 2. Use Newton's binomial theorem to compute 30 to 4...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

solve all parts have not been understanding it, precise answers with explanations on how to arrive at the answer please Exercise 3.12. Three players, Avinash, Brian and John, play the following game....

1 Program descriptions You will write six programs for this project. Except where explicitly noted, your programs may assume that their inputs are properly formatted. However, your programs should be...

Possible Multiple Choice Questions for the Exam. Focus on the topics discussed in class. Chapter 1 Multiple Choice Identify the choice that best completes the statement or answers the question. ____...

PLEASE answer these U (1) Encrypt the message WATCH YOUR STEP by translating the letters into numbers, applying the given encryption function, and then translating the numbers back into letters. (a)...

The Slide Game in Python In this assignment, you will be writing Python code for the Slide Game. Instead of using colourful pictures of squares on a game board (as we saw in the last section), in our...

Remaining Time: 2 hours, 10 minutes, 00 seconds. Question Completion Status: QUESTION 1 Use the following information on Company and perform proforma financial modeling using a planned expansion...

QUESTION 3 (20 Marks) a) Discuss with the example three conceptual approaches to probability. (6 Marks) b) A traffic management company wants to conduct a study on proportion of trucks that use a...

Return to Targets 2010 annual report. For instructions on how to access the report online, see the Continuing Financial Statement Analysis Problem in Chapter 2. On page 33 of the annual report, youll...

Donald Barker, a wealthy Oregon resident, went to the law firm Winokur, Schoenberg, Maier, Hamerman & Knudson to have his estate planned. An attorney at the firm repeatedly told Barker that he could...

the required rate of return increases. the initial capital requirement increases. some of the cash inflows are deferred until a later year. the aftertax salvage value of the fixed assets increases....

On March 1, 2015, Cain Company issued at 103 plus accrued interest 4,000 of 9%, P1,000 face value bonds. The bonds are dated January 1, 2015 and mature on January 1, 2029. Interest is payable...