Question: Let P R be a column stochastic matrix. Show that any eigenvector v corresponding to an eigenvalue # 1 satisfies v - 1,, =

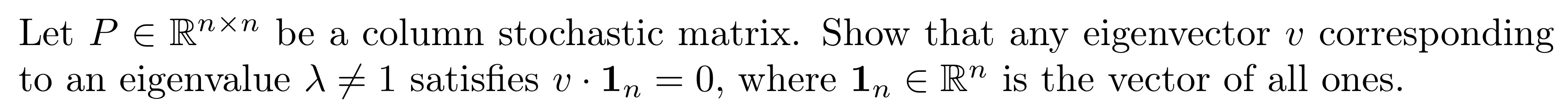
Let P R be a column stochastic matrix. Show that any eigenvector v corresponding to an eigenvalue \\ # 1 satisfies v - 1,, = 0, where 1,, R is the vector of all ones

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Problems : 9,11,24,25,26 Direction : in the exercices 9 and 11 find a basis for the eigenspace corresponding to each listed eigenvalueHello can I have some help here please. Can you write on a sheet...

A DEMO OF GOOGLE PAGE RANK Google has changed the conventional business mode and its success derives in large part from its PageRank algorithm, which ranks the importance of webpages according to an...

A matrix A R n,n is said to be nonnegative (resp. positive) if a ij 0 (resp. a ij > 0) for all i, j = 1, . . . , n. The notation A 0 (resp. A > 0) is used to denote nonnegative (resp. positive)...

5. [1+1+2pt] The Google page rank algorithm has a lot to do with the eigenvector corre- sponding to the largest eigenvalue of a so-called stochastic matrix, which describes the links between...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Questions 5 - 6 and 7 1. PANDEMIC WITH SIR MODEL Covid19 is changing you and me, and the entire world. Where are we heading to? What does our future life look like? All the answer shall rely on the...

Long Question: Markov chain In many applications, some variables evolve over time in a random (stochastic) way in that even if you know everything up to time t, it is still impossible to know for...

I'm stuck in the question solve this question quickly 5. The next problems discuss eigenvalues and eigenvectors of stochastic matrices. Stochastic matrices are very useful for ranking sport teams or...

1. Let 1 and 2 be two symmetric, positive definite matrices. Let A be a diagonal matrix containing the eigenvalues of 2. Let A contain the corresponding eigenvectors of 2 as its rows in the same...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials...

Find the constants B and n in Chvorinov's rule by plotting the following data on a log-log plot: Casting dimensions (in.)Solicitation time (min) 0.5 ( 8 ( 12......................3.48 2 ( 8 (...

Christopher's Closet sells men's clothing. At the end of the current year. Christopher's Closet has Rent Expense of $1,500, and Supplies Expense of $829. What closing entry will Christopher's Closet...

What is the process of deciding whether or not to extend credit to a particular customer called? Multiple choice question. debit analysis default analysis credit analysis customer analysis

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...