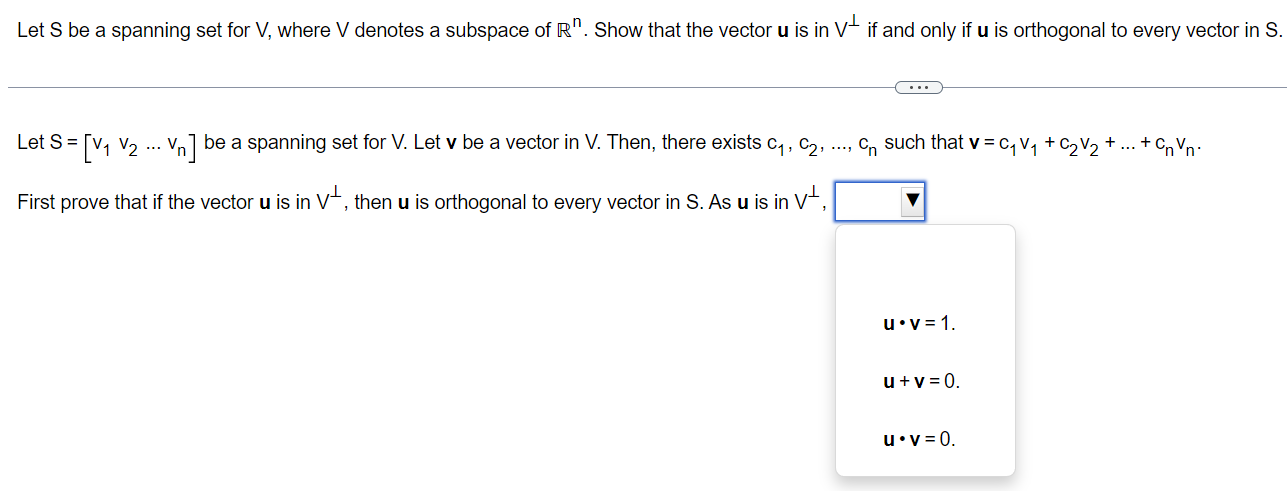
Let S be a spanning set for V. where V denotes a subspace of R". Show that the vector u is in Vi if and only if u is orthogonal to every vector in S. Let S = [v1 v2 vn] be a spanning set for V. Let v be a vector in V. Then, there exists c1, 02, on such that v = c1v1 + c2v2 + + cnvn. First prove that if the vector u is in Vi, then u is orthogonal to every vector in 3. As u is in Vi, I3