answer given questions showing all work

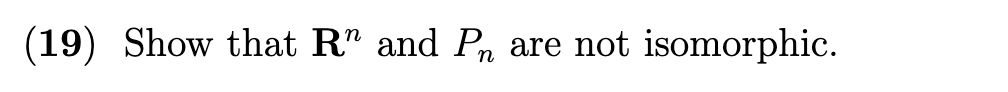
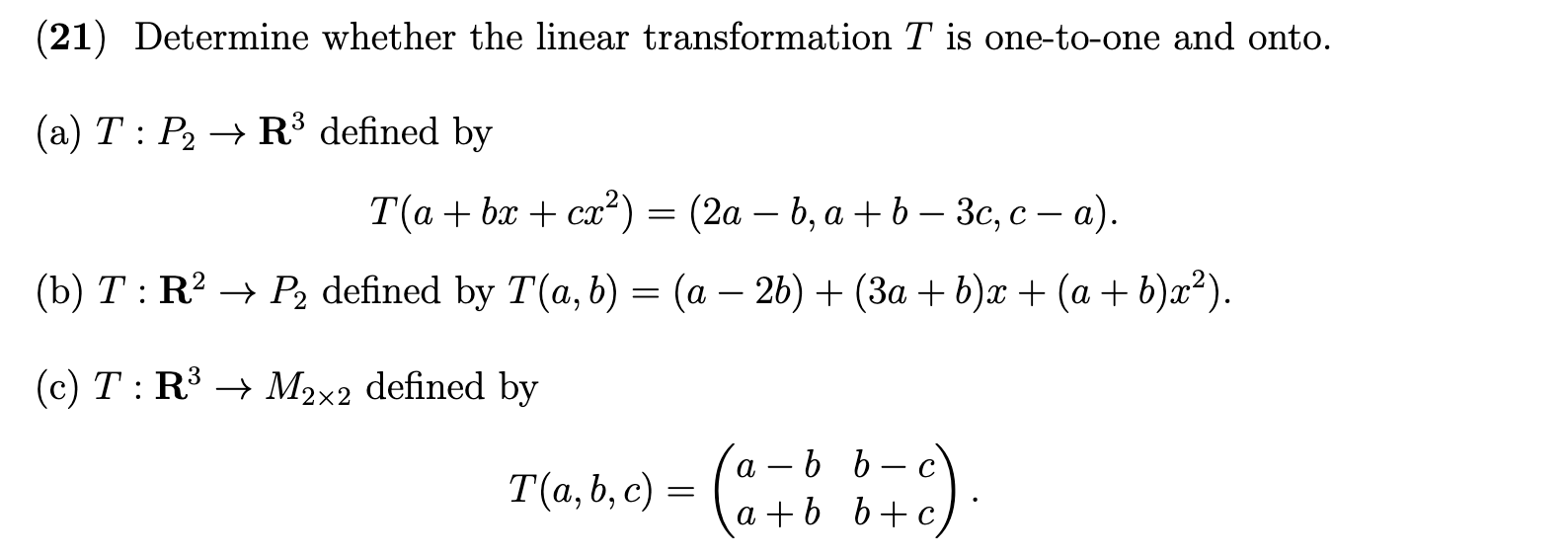
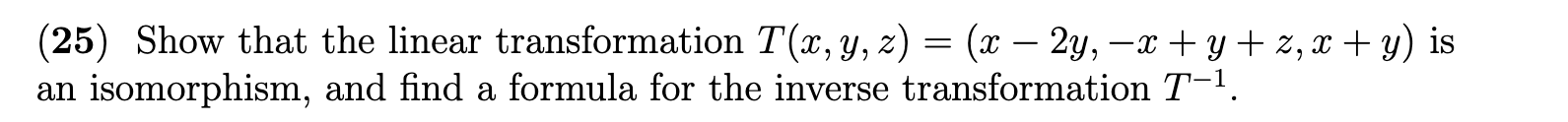
(2) Let T : V > W be a linear transformation, and let S be a subspace of V. Prove that the set T(S) = {0: E W|T() = o: for some 6 E S} is a subspace of W. (9) Are the following transformations (a) T : M2x2 - R defined by T(A) = det( A). (b) T : R -+ R defined by T(x) = 27. (c T : R - R defined by T(x) = x+1. linear?(10) Let T : V > W be a linear transformation and let B = {a1,a2, . . . ,an} be a spanning set for V. Prove that the set T(B) = {T(a1),T(oz2), . . . ,T(an)} spans the range of T. \f(14) Let T : V > W be a linear transformation. Prove that if S = {(11, a2, . . . ,an} is a linearly independent set in V, then the set T(S) = {T(a1),T(a2), . . . ,T(ozn)} is linearly independent in W. (21) Determine whether the linear transformation T is one-to-one and onto. (a) T : P2 - R3 defined by T(a t bx + cx2) = (2a - b, a + b - 3c, c- a). (b) T : R2 + P2 defined by T(a, b) = (a - 2b) + (3a + b)x + (a + 6)x2). (c) T : R3 + M2x2 defined by a- b b- c T(a, b, c) = atb bt c(25) Show that the linear transformation T(x, y, z) = (x - 2y, -x ty + z,x ty) is an isomorphism, and find a formula for the inverse transformation T