Question: Let S be the circle in the x-y plane defined by the equation x + y = 4. Let P be a point on

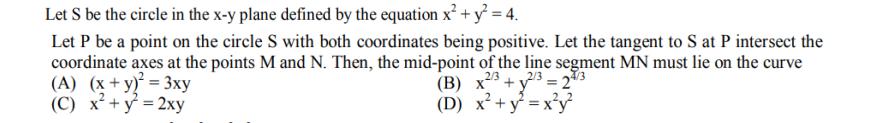
Let S be the circle in the x-y plane defined by the

Let S be the circle in the x-y plane defined by the equation x + y = 4. Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve (A) (x + y) = 3xy 2/3 (B) x2 + y2/3=1 = 24/3 (D) x + y = xy 2 (C) x + y = 2xy

Step by Step Solution

★★★★★

3.36 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The detailed ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let S be the sample space for an experiment and let A, B with A B. Prove that Pr(A)

Let S be the sample space for an experiment , with events A, B Prove that PrA PA)+Pr(B)1 Pr(B)

Let S be the sample space for an experiment E. If A, B are events from S with A B = S, A B = , Pr(A) = p, and Pr(B) = p2, determine p.

In Problems 1-3, find the equation of the tangent plane to the given surface at the indicated point. 1. x2 + y2 + z2 = 16; (2, 3, (3) 2. 8x2 + y2 + 8z2 = 16; (1, 2, (2/2) 3. x2 - y2 + z2 + 1 = 0; (1,...

Fill in each blank so that the resulting statement is true. The midpoint of a line segment whose endpoints are (x 1 , y 1 ) and (x 2 , y 2 ) is (______ ,_________ ).

Use implicit differentiation to find the equation of the tangent line to the curve x2 + y2 / 4 = 1 at the point (- (3 / 2, 1)?

Let S be the hyperboloid x 2 + y 2 = z 2 + 1 and let P = (, , 0) be a point on S in the (x, y)-plane. Show that there are precisely two lines through P entirely contained in S (Figure 18). Consider...

(a) A direction field for the differential equation y' = x2 - y2 is shown. Sketch the solution of the initial-value problem y' = x2 - y2 y(0) = 1 Use the graph to estimate the value of y(0.3). (b)...

Sketch each of the following sets. Identify which of the following sets are open, which are closed, and which are neither. Also discuss the connectivity of each set. a) E = {(x, y): y 0} b) E = {(x,...

For each of the following sets, sketch E, , and E. a) E = {(x, y) : x2 + 4y2 x2, 0

(a.) Estimating a single index model with four observations has revealed the following results: Rit = 2.473 + 1.011 Rmt + Eit The four market returns used in the estimation were: 9%, 5%, -1% and -3%...

Call Provisions a company is contemplating a long-term bond issue. It is debating whether to include a call provision. What are the benefits to the company from including a call provision? What are...

( 1 point ) Find the solution t o the initial value problem ( 1 + x 1 0 ) y ' + 1 0 x 9 y = 2 0 x 9 subject t o the condition y ( 0 ) = 2 .

Dana Company reported the following amounts in the stockholders equity section of its December 31, 2006 balance sheet: Preferred stock, 9%, $100 par (10,000 shares authorized, 1,000 shares issued) ....

What are the main steps in carrying out sentiment analysis projects? Discuss.

The following determination and distribution of excess schedule is prepared on January 1, 2012, the date on which Parker Company purchases a 60% interest in Share Company: On December 31, 2013,...

Jamel Blanton was a male employee at a Pizza Hut restaurant operated by Newton Associates, Inc., in San Antonio, Texas. Blanton was subjected to sexual and racial harassment by the general manager,...

Local cable television companies are sometimes granted monopoly rights to service a particular territory of a metropolitan area. The companies typically pay special taxes and licensing fees to local...

El ritmo incremental de las ventas fortalece las expectativas de beneficios que, junto a una favorable oferta de crdito, inducen una expansin ms que proporcional del gasto en inversin neta: crece el...

Let L be the circle in the x-y plane with center the origin and radius 95. Let S be a moveable circle with radius 85 . S is rolled along the inside of L without slipping while L remains fixed. A...

Let L be the circle in the xy plane with center the origin and radius 76. Let S be a moveable circle with radius 64 . S is rolled along the inside of L without slipping while L remains fixed. A point...

Need Detailed Explanation of Bonus 3,4, D,F,E and there parts on Paper D Bonus 3 Choose one of the below. An extra page has been left for workspace if you feel you need to use it. 40 pts 1) Let F =...

Need Detailed Solution on Paper please clear formatting easy to understand please. for Bonus 3,4,D,E,F and there parts. Everything is mentioned on the paper kindly read it D Bonus 3 Choose one of the...

Packing circles and rectangles Description In this assignment, you are asked to implement a program (named checkpack ) that, given a rectangular domain and a list of circles and rectangles, can check...

In this assignment, you are asked to implement a program (named checkpack) that, given a rectangular domain and a list of circles and rectangles, can check if the packing configuration is valid, in...