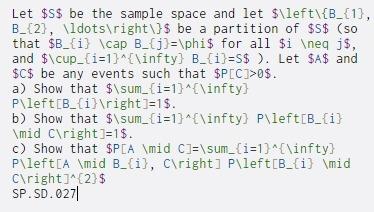
Let $S$ be the sample space and let $\left\{B_{1}, B_{2}, \ldots ight\}$ be a partition of $5$ (so that $B_{i} \cap B_{j}=\phi$ for all $i eg js, and $\cup_{i=1}^{\infty) B_{i}=5$). Let $A$ and $C$ be any events such that $P[C]>0$. a) Show that $\sum_{i=1}^{\infty) P\left [B_{i} ight)=1$. b) Show that $\sum_{i=1}^{\infty) P\left [B_{i} \mid C ight)=1$. c) Show that $PCA \mid C]=\sum_{i=1}^{\infty? P\left(A \mid B_{i}, C ight] P\left(B_{i} \mid C ight)^{2} $ SP.SD.027