Let (S, dS) be the unit 2-sphere and G be its isometry group. We define a metric dG on G by dG(g1, g2) = max x?S dS(g1x, g2x). (The maximum can be attained because x 7? dS(g1x, g2x) is a continuous function over S. Btw, S being a sphere here is not important; in general, S can be replaced by any compact metric space.) Show that (1) dG is indeed a metric on G. (2) dG(hg1, hg2) = dG(g1, g2) for all g1, g2, h ? G. (3) dG(g1h, g2h) = dG(g1, g2) for all g1, g2, h ? G

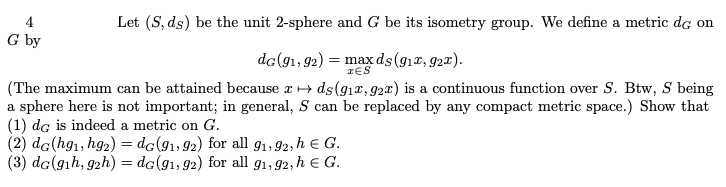
4 Let (S, ds) be the unit 2-sphere and G be its isometry group. We define a metric do on G by do(91, 92) = max ds (91I, 921). IES (The maximum can be attained because x -> ds(91, 921) is a continuous function over S. Btw, S being a sphere here is not important; in general, S can be replaced by any compact metric space.) Show that (1) do is indeed a metric on G. (2) do(hg1, hg2) = do(91, 92) for all 91, 92, he G. (3) do(gih, gzh) = do(91, 92) for all g1, 92, he G