Question: Let SW AP ( L ) = { ywx | xwy in L , x , y in Sigma , w in Sigma
Let SW AP Lywx xwy in L x y in Sigma w in Sigma ie the set of strings from L
but with their first and last letters swapped. This means that if L cat dog then
SW AP Ltac god
Prove that if L is a regular language, then SW AP L must also be regularLet SWAPyinwin ie the set of strings from
but with their first and last letters swapped. This means that if dog then
god
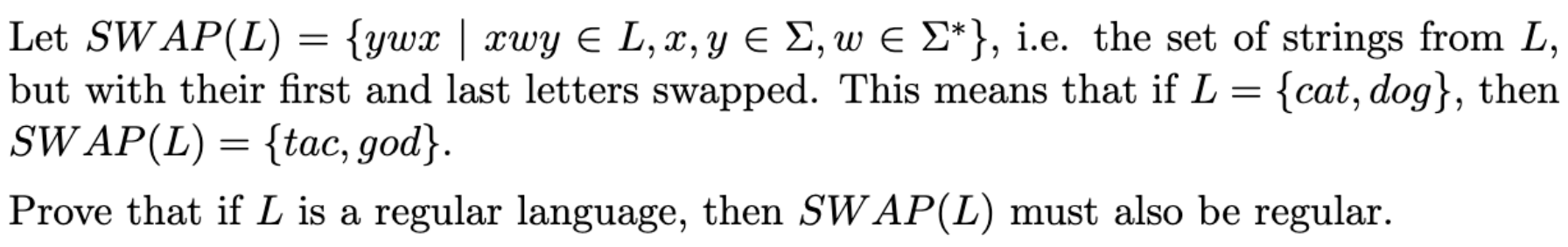
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


