Let T be a binary tree with n vertices. Deleting any vertex v splits T into at most three subtrees, containing the left child of v(if any), the right child of v(if any), and the parent of v(if any). We call v a central vertex if each of these smaller trees has at most n/2 vertices. See the figure below for an example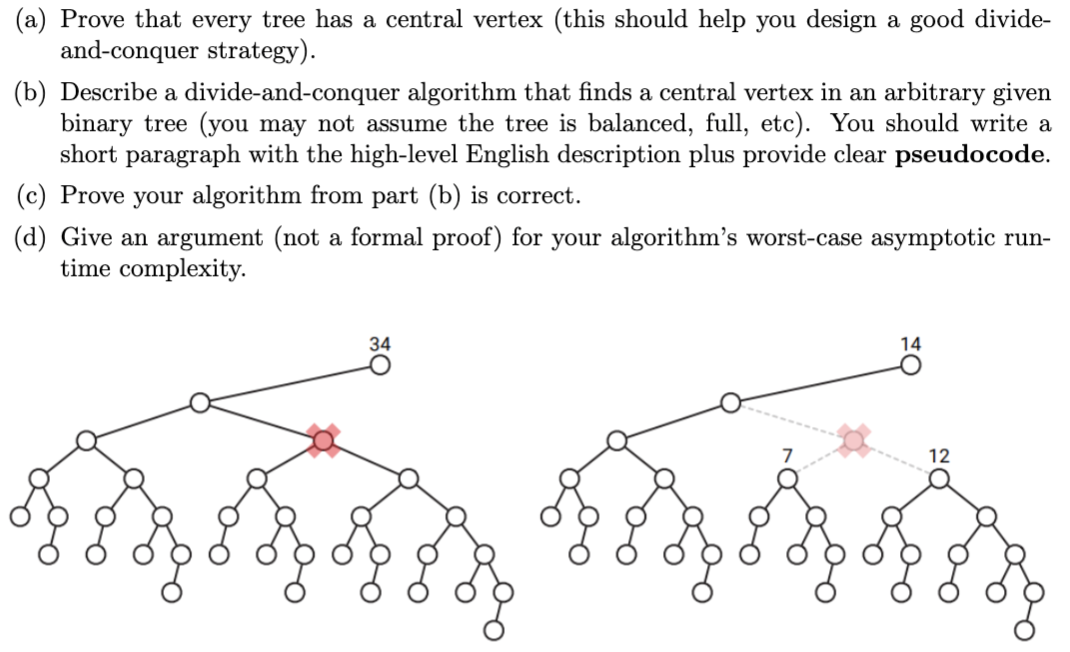

(a) Prove that every tree has a central vertex (this should help you design a good divide- and-conquer strategy). (b) Describe a divide-and-conquer algorithm that finds a central vertex in an arbitrary given binary tree (you may not assume the tree is balanced, full, etc). You should write a short paragraph with the high-level English description plus provide clear pseudocode. (c) Prove your algorithm from part (b) is correct. (d) Give an argument (not a formal proof) for your algorithm's worst-case asymptotic run- time complexity. 34 14 7 12 (a) Prove that every tree has a central vertex (this should help you design a good divide- and-conquer strategy). (b) Describe a divide-and-conquer algorithm that finds a central vertex in an arbitrary given binary tree (you may not assume the tree is balanced, full, etc). You should write a short paragraph with the high-level English description plus provide clear pseudocode. (c) Prove your algorithm from part (b) is correct. (d) Give an argument (not a formal proof) for your algorithm's worst-case asymptotic run- time complexity. 34 14 7 12