Question: Let $T: R^{2} ightarrow R^{2}$ be the linear operator defined by $$ Tleft(left[begin{array}{1} X_{1} W X_{2} end{array} ight] ight)=left[begin{array}{1} 8 x_{1}-x_{2} 8 x_{1}+x_{2} end{array} ight]

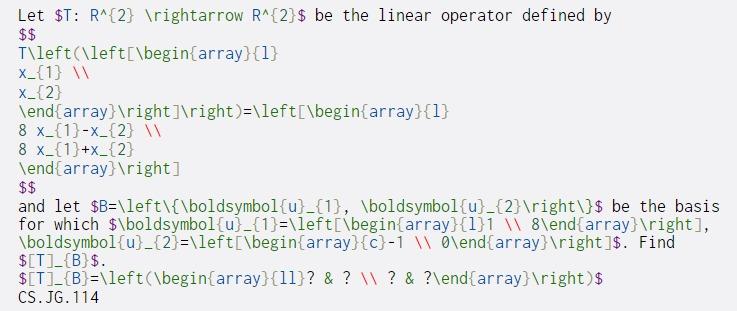
$Let $T: R^{2} ightarrow R^{2}$ be the linear operator defined by$

Let $T: R^{2} ightarrow R^{2}$ be the linear operator defined by $$ T\left(\left[\begin{array}{1} X_{1} W X_{2} \end{array} ight] ight)=\left[\begin{array}{1} 8 x_{1}-x_{2} 8 x_{1}+x_{2} \end{array} ight] $$ and let $B=\left\{\boldsymbol{u}_{1}, \boldsymbol{u} _{2} ight\}$ be the basis for which $\boldsymbol{u} _{1}=\left[\begin{array}{1}1 \\ 8\end{array} ight], \boldsymbol{u} _{2}=\left[\begin{array}{c}-1 O\end{array} ight]$. Find $[T]_{B}$. $[T]_{B}=\left(\begin{array}{11}? & ? ? & ?\end{array} ight) $ CS.JG. 114

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Let $T: R^{2} ightarrow R^{2}$ be the linear operator defined by $$ T\left(\left[\begin{array}{1} x_{1} \ X_{2} \end{array} ight] ight)=\left[\begin{array}{1} 8 x_{1}-x_{2} \ 8 x_{1}+x_{2}...

Let $T: R^{2} ightarrow R^{3}$ be defined by $T=\left(\left[\begin{array} {1}x_{1} \\x_{2} \end{array} ight] ight)=\left [\begin{array}{c}x_{1}+2 x_{2} \ -x_{1} \\ \end{array} ight]$ Find the matrix...

Let $T: R^{2} ightarrow R^{3}$ be defined by $T=\left(\left[\begin{array} {1}x_{1} \\x_{2} \end{array} ight] ight)=\left[\begin{array}{c}x_{1}+8 x_{2} \ -x_{1} \\ \end{array} ight]$ Find the matrix...

Let $T: R^{2} ightarrow R^{3}$ be defined by $T=\left(\left[\begin{array} {1}x_{1}x_{2} \end{array} ight] ight)=\left[\begin{array}{c}x_{1}+2 x_{2} \ -x_{1} 1 O\end{array} ight ]$ Find the matrix...

If $T_{1}: V ightarrow 1$ and $T_(2): V ightarrow V$ are two linear transformations. Then, which of the following is not a linear transformation? a. $T_{1}+T_{2}$ b. $\alpha T_{1}$ c. $T_{1} \circ...

Let $B=\{(1,2),(-1,-1) \}$ and $B^{\prime} =\{(-4,1),(0,2)\}$ be bases for $R^{2}$, and let $A=\left[\begin{array}{rr}0 & 2 1 -1 & 1\end{array} ight]$ be the matrix for $T: R^{2} ightarrow R^{2}$...

Let $B=\{(1,2), (-1,-1)}$ and $B^{\prime) =\{(-4,1),(0,2)\}$ be bases for $R^{2}$, and let $A=\left[\begin{array}{rr}0 & 2 1 -1 & 1\end{array} ight]$ be the matrix for $T: R^{2} ightarrow R^{2}$...

Consider the following data taken on subgroups of size 5. The data contain 20 averages and ranges on the diameter (in millimeters) of an important component part of an engine. Display X- and...

A circuit contains a 175- resistance, a 2.50F capacitor, and a 62.0-mH inductance in series with a 110-V, 60.0-Hz source. Find the impedance and the current.

A _ _ _ _ _ _ _ _ allows an investment banker to purchase up to 1 5 % of additional shares in an equity offering beyond what is offered to the public.

required return green company: 12.4% red inc: 6.1% gold corp: 10.2% Stock Valuation and Required Return Green Company, Red, Incorporated, and Gold Corporation each will pay a dividend of $3.50 next...

10. Does your organization maintain a committee charged with improving the working climate for all employees?

9. Are there consequences for colleagues who engage in demeaning or prejudicial behavior toward others?

5. What advice might Hayward take from Drucker (cited toward the beginning of this chapter) to improve his success in the future?