Question: Let T: R R* be a linear transformation defined by T X y Z W = -2x+3y-z+w x+4y+3z-3w x-7y-2z+2w 11y + 5z-5w (a) Find

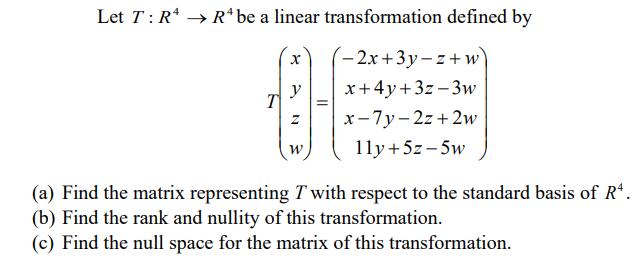
Let T: R R* be a linear transformation defined by T X y Z W = -2x+3y-z+w x+4y+3z-3w x-7y-2z+2w 11y + 5z-5w (a) Find the matrix representing Twith respect to the standard basis of R. (b) Find the rank and nullity of this transformation. (c) Find the null space for the matrix of this transformation.

Step by Step Solution

★★★★★

3.33 Rating (150 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

SOLUTION a To find the matrix representing T with respect to the standard basis of R4 we need to apply the transformation T to each basis vector 1 0 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Management Leadership Questions!

Larned Recreational builds two models of dune buggies: Sport and Custom. Both models require the same assembly and finishing process and are assembled in the same factory. They differ in the quality...

One hears the comment, its only a theory in regard to scientific theories such as the age of the earth, climate change, the theory of evolution, the theory of plate tectonics. after reading chapter...

Two containers are taken such that capacity of first is one tenth of second. In both of them, 3 litres of milk and 7 litres of water is added. Now, from second container, 4 litres of the mixture is...

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Ryan Ren Assignment Homework 2 due 09/14/2017 at 02:15pm PDT 1. (1 pt) Compute the following product. \u0014 \u0015\u0014 \u0015 \u0014 5 0 4 7 4 = 0 7 1 7 7 Math4A-02-M17-Wen \u0015 Answer(s)...

THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS JUNE 2015 MATH2501 Linear Algebra (1) TIME ALLOWED - THREE HOURS. (2) TOTAL NUMBER OF QUESTIONS - 5 (3) ANSWER ALL QUESTIONS (4)...

THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS JUNE 2016 MATH2501 Linear Algebra (1) TIME ALLOWED - THREE HOURS. (2) TOTAL NUMBER OF QUESTIONS - 5 (3) ANSWER ALL QUESTIONS (4)...

1) Consider f : P2 - P2 defined by T[f (c)] = cand T[f (x)] = f(x + 2), f(x) EP2. Find the matrix of T with respect to the standard basis and the basis {x- + x + 1, x, 1} 2) Check whether the...

QS 10-19A (Algo) Computing bond price C2 Compute the selling price of 10%, 10-year bonds with a par value of $380,000 and semiannual interest payments. The annual market rate for these bonds is 12%....

Why is the case of Haig v. Bamford considered important in the recent development of tort law?

Open Kellogg's Annual Reports and find the Consolidated Statement of Earnings. What was interest expense in the last two years?

5e_BSBTWK502 Provide one example of how you have acted on information from line management

Kristi Williams offers family counseling services specializing in financial and marital problems. Kristi Williams Family Counseling Services UNADJUSTED TRIAL BALANCE December 31, 20-- ACCOUNT TITLE...

The Electrocomp Corporation manufactures two electrical products: air conditioners and large fans. The assembly process for each is similar in that both require a certain amount of wiring and...

You are the business manager for Indy Deck Builders, a local construction company that specializes in new deck installation. Your company offers three-deck models. Model A which costs $2,000, model B...

1. Assume the role of a prospective buyer for these two businesses. How would you conduct the due diligence necessary to determine whether they would be good investments?

A professor suggests that her college students will attend class more if quizzes were given in every class. To demonstrate the need for this change, the professor records the attendance of students...

When selecting characteristics for performance evaluation of hourly paid workers, which of the following characteristics should typically be prioritized to enhance organizational effectiveness?...

Show how to modify the Bellman-Ford algorithm slightly so that when we use it to solve a system of difference constraints with m inequalities on n unknowns, the running time is O(n m).

Prove that for any directed graph G, we have ((G T ) SCC ) T = G SCC . That is, the transpose of the component graph of GT is the same as the component graph of G.

Suppose that you are the general manager for a major-league baseball team. During the off-season, you need to sign some free-agent players for your team. The team owner has given you a budget of $X...

Wasatch Corp. (WC) received a $200,000 dividend from Tager Corporation (TC). WC owns 15 percent of the TC stock. Compute WC's deductible DRD in each of the following situations: a. WC's taxable...

Last year, BTA Corporation, a calendar-year taxpayer, reported a net operating loss of ($10,000) and a $0 tax liability. BTA confidently anticipates a current year tax liability of $240,000. What...

Assume Maple Corp. has just completed the third year of its existence (year 3). The table below indicates Maple's ending book inventory for each year and the additional 263A costs it was required to...