Let the () and () matrices be defined as below on LU factorization and suppose R is invertible.

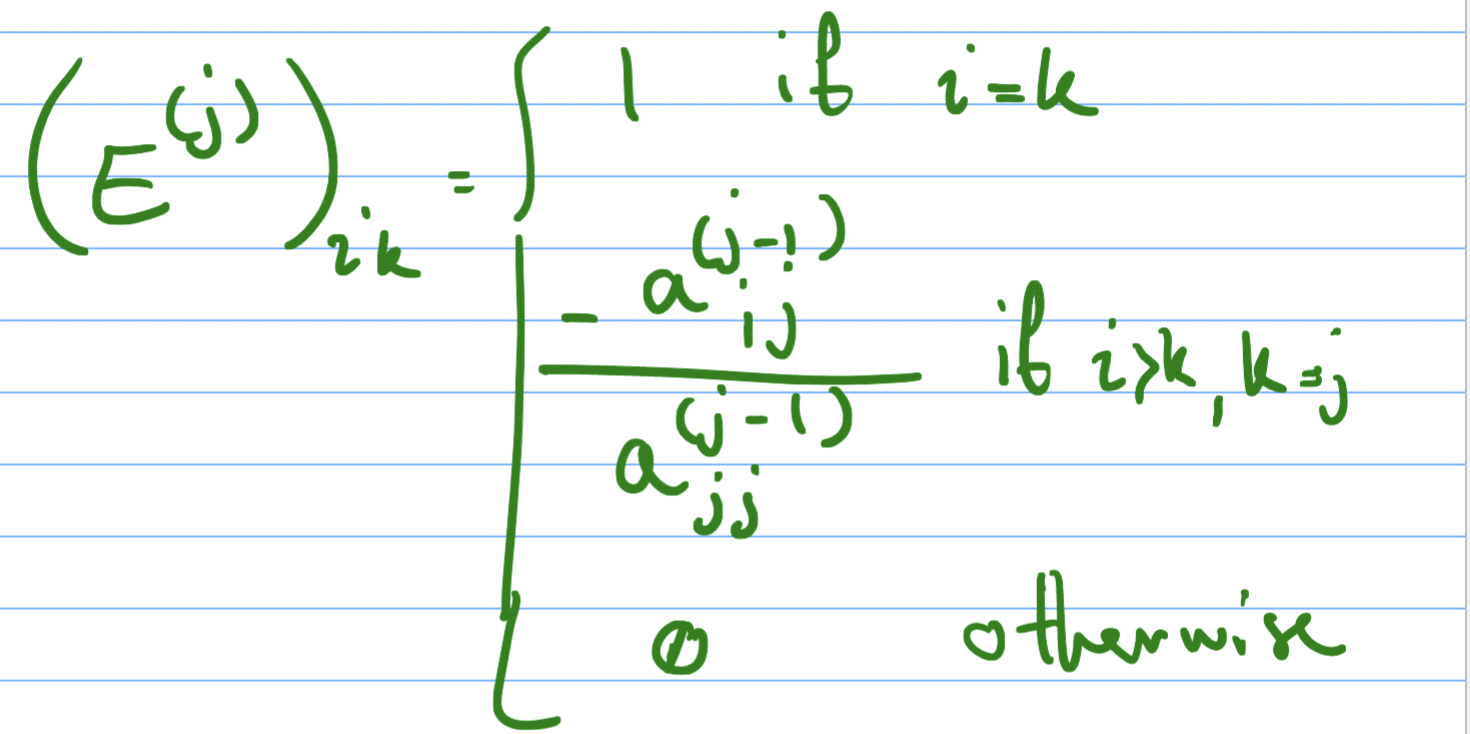
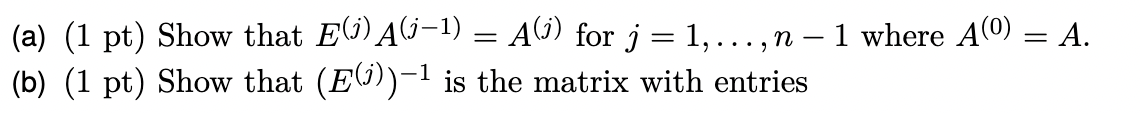
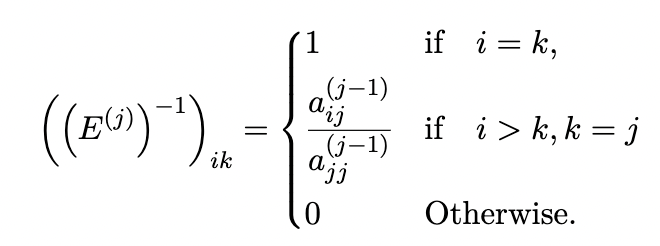
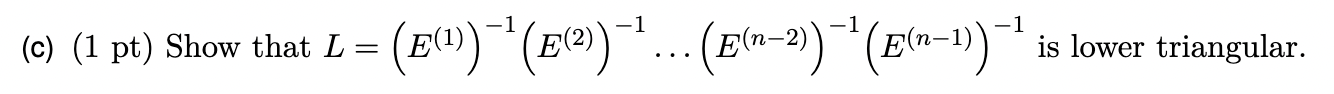
(E(j))ik=1ifajj(j1)aij(j1)0i=kibi>k,kjjotherwise (a) (1 pt) Show that E(j)A(j1)=A(j) for j=1,,n1 where A(0)=A. (b) (1 pt) Show that (E(j))1 is the matrix with entries ((E(j))1)ik=1ajj(j1)aij(j1)0ifi=k,ifi>k,k=jOtherwise. that L=(E(1))1(E(2))1(E(n2))1(E(n1))1 is (E(j))ik=1ifajj(j1)aij(j1)0i=kibi>k,kjjotherwise (a) (1 pt) Show that E(j)A(j1)=A(j) for j=1,,n1 where A(0)=A. (b) (1 pt) Show that (E(j))1 is the matrix with entries ((E(j))1)ik=1ajj(j1)aij(j1)0ifi=k,ifi>k,k=jOtherwise. that L=(E(1))1(E(2))1(E(n2))1(E(n1))1 is